19. Системы одновременных уравнений

В такой системе одни и те же переменные системы рассматриваются одновременно как объясняемые в одном и том же уравнении и как объясняющие в остальных уравнениях.Виды систем уравнений:

1) система независимых уравнений.Каждый результативный признак(объясняемая переменная) yj,где j=1,n является функцией одной и той же совокупности факторов xi, где i=1,m.Набор факторов в каждом уравнении системы может изменяться в зависимости от изучаемого явления.

2) система рекурсивных уравнений.Результативный признак yj,где j=1,n одного уравнения системы в каждом последующем уравнении является фактором наряду с одной и той же совокупностью факторов xi, где i=1,m.

3)система одновременных уравнений.Результативный признак yj,где j=1,n одного уравнения системы входит во все другие уравнения системы в качестве фактора наряду с одной и той же совокупностью факторов xi, где i=1,m.

Систему независимых или рекурсивных уравнений решают с помощью МНК.Для решения системы одновременных уравнений требуются другие,отличные от МНК методы.Системы совместных уравнений представляют наибольший практический интерес.такие системы эффективны в эконометрических исследованиях и наиболее широко применяются в макроэкономике.

Структурная форма модели:

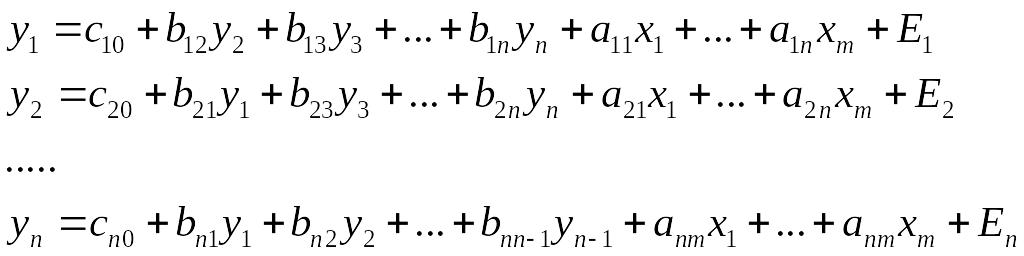
Содержание параметров структурной формы модели

Параметр	Содержание параметра
, где , где , , где ,	Свободный член ур-ния модели Коэф-т при эндогенной переменной Коэф-т при экзогенной переменной

Виды переменных:

-эндогенные переменные(y) определяются внутри модели и являются зависимыми переменными;

-экзогенные переменные(x) определяются вне системы и являются независимыми переменными. Предполагается,что они не коррелируют с ошибкой в соответствующем уравнении;

-предопределенная-экзогенные и лаговые(за предыдущие моменты времени)эндогенные переменные этой системы.

Классы структурных уравнений модели:

1Поведенческие уравнения. Описывают взаимодействия между эндогенными и экзогенными переменными;

2Тождества. Устанавливают соотношение между эндогенными переменными,не содержат случайных составляющих и структурных коэффициентов модели.

Структурная форма модели может быть преобразована в приведённую форму:

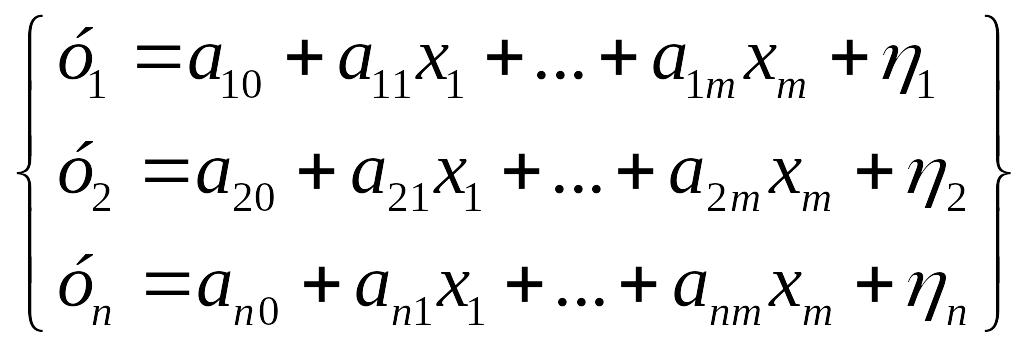
Параметр. (коэф приведенной модели)	Содержание параметра.
, где , где ,	Свободный член ур-ния сис-мы. Коэф при предопределенной переменной явл ф-цией коэф стр-ной формы модели.

Причины построения приведённой формы модели:

1оценки параметров структурной формы модели, найденные с помощью МНК являются смещенными и несостоятельными(нарушаются предпосылки МНК) в силу того,что эндогенные переменные коррелируются со случайными отклонениями;

2независимость уравнений в приведённой форме модели позволяет определить состоятельные оценки её параметров с помощью МНК;

3параметры(коэффициенты) приведённой формы модели связаны с параметрами её структурной формы.