17.Стационарный врем.Ряд

Временный ряд наз стационарным, если закон распределения и его числовые хар-ки не зависят от t. Тогда математическое ожидание и среднее квадратическое отклонение могут быть оценены по формулам:

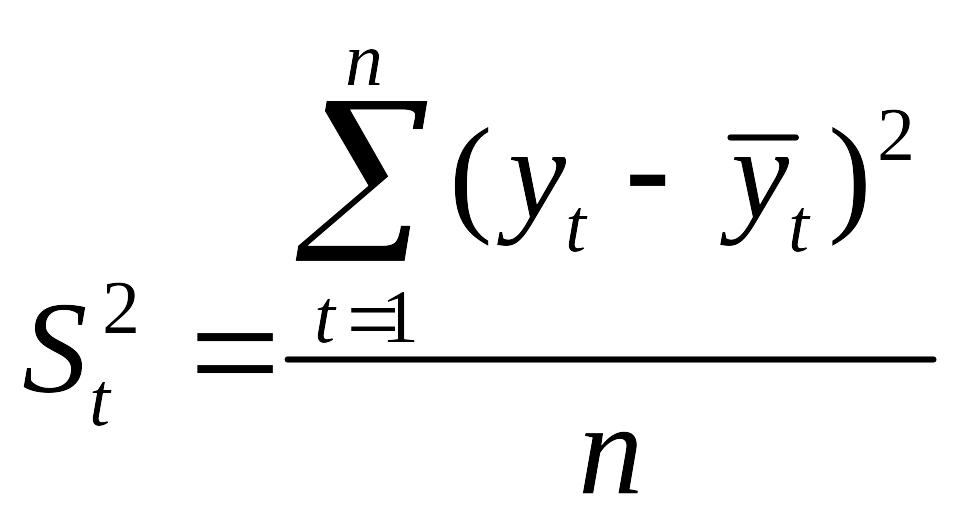
Стационарным временным рядом в широком смысле (слабо стационарным), наз случайный процесс у кот среднее значение, дисперсия и автокорреляционн.ф ф-ция не зависят от t.

Степень тесноты связи м/у последовательностями наблюдений временного ряда, сдвинутыми относительно др. др. на ед. (с лагом )может быть определена с помощью коэф корреляции.

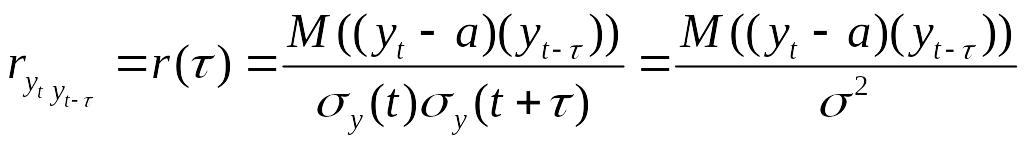
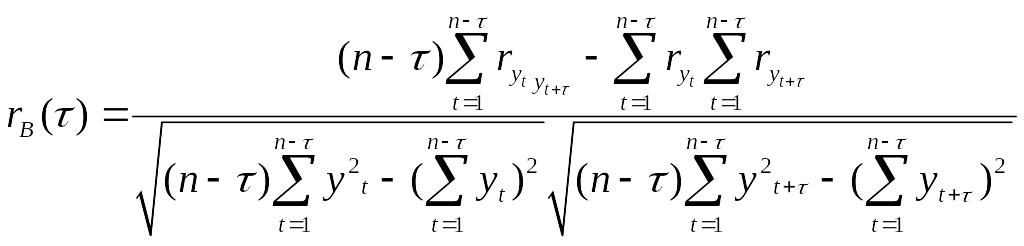
Ф-цию r_B=( ) наз выборочной автокорреляционной ф-цией, а ее график – коррелограммой. Одной из важнейших задач исследования экономического временного ряда явл выявление основной тенденцией изучаймого процесса.

Понятие об авторегрессионных моделях.

Авторегрессионная модель р-го порядка (или модель AR(р)) имеет вид.

Она описывает изучаемый процесс в момент t в зависимости от его значений в предыдущие моменты.

Важное значение в анализе ВР имеют стационарные ВР, вероятностные св-ва кот-ых не изменяются во времени. ВР yt (t=1,2,..,n) наз. стационарными, если совместное распределение вероятностей p наблюдений y1,y2,y3,...,yn такое же,как и p наблюдений y1+τ, y2+τ,yn+τ, при любых p и τ. Тогда математическое ожидание и среднее квадратическое отклонение могут быть оценены по формулам:

То есть св-ва стацион рядов не зав от t.Коэффициента автокорр-ции. Степень тесноты связи м/у компонентами ВР yt (сдвинутых относит-но друг друга на τ-единиц,или как говорят, с лагом τ)может быть определена с пом коэффициента корреляции: , Т.к. коэфф.r(τ,t) измеряет корреляцию м/y членами одного и того же ВР, его наз. коэфф. автокорр-ции.Для стационар времен ряда коэ-т авток-ции не зав от t. Зависимость r(τ)-также наз. автокорр-ционной ф-ей. В силу стационарности ВР yt(t= ) автокорр-ая ф-я зависит только от лага τ,причем r(-τ)=r(τ).

18. Типы трендов временных рядов. Авторегрессионные модели+17(концовка)

Основные типы трендов). Тенденции изменения показателей сложных общественных явлений только приближенно можно выразить тем или иным уравнением, линией тренда. На практике чаще всего используют следующие основные типы трен­дов временных рядов: прямолинейный, параболический, экспо­ненциальный, гиперболический и др.

Для определения параметров функции тренда f(t) чаще всего используется метод наименьших квадратов. Значения временного ряда , рассматриваются как зависимая переменная, а время t - как объясняющая: y_t=f(t) + e_t,

где е, - возмущения, удовлетворяющие основным предпосылкам регрессионного анализа, т. е. представляющие собой независимые и одинаково распределенные случайные величины, распределение которых предполагается нормальным.

Напомним, что, согласно методу наименьших квадратов, па­раметры зависимости f(t) = b₀ + b1t находятся из системы нормальных уравнений

Линейный тип тренда подходит для отображения тенденции примерно равномерного изменения уровней: равных в среднем ве­личин абсолютного прироста или абсолютного сокращения уров­ней равные промежутки времени.

Экспоненциальный и степенной тренды характерны для процессов, развивающихся в среде, не создающей никаких ограниче­ний для роста уровней. На практике такие явления встречаются только в ограниченном промежутке времени, поскольку любая среда рано или поздно создает ограничения.

Методом выравнивания (сглаживания) временного ряда, т. е. выделения неслучайной составляющей, является метод сколъзящих средних. Он основан на переходе от начальных значений чле-в1ш ряда к их средним значениям на интервале времени, длина ко­нного определена заранее.