15. Гетероскедатичность.Графический анализ отклонений.

Гетероскедастичность

Зависимость потребления от дохода

1. дисперсия потребления остается одной и той же для различных уровней дохода

2. дисперсия потребления увеличивается с ростом дохода

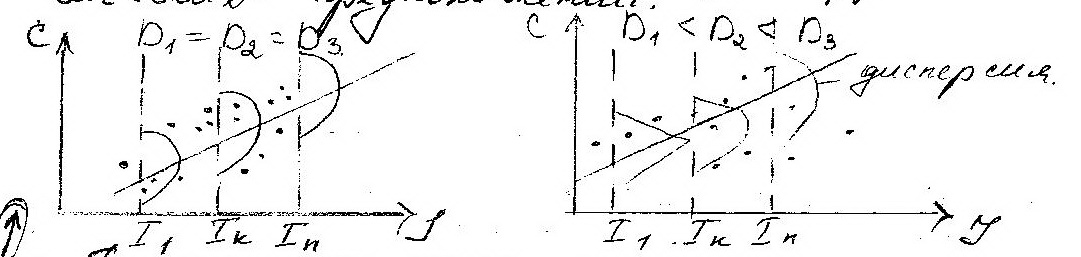
Последствия гетероскедастичности:

1. оценки коэф по-прежнему останутся несмещенными и линейными

2. неэффективно

3. дисперсия рассчитывается со смещением

4. выводы ненадежны

Одной из осн предпосылок МНК явл условие постоянства дисперсий случ отклонений. Выполнимость – гомоскедатичность, невыполнимость – гетероск.(непостоянство дисперсий отклонений).Проблема в осн хар-на при исп-нии перекрестных данных. Последствия гетероскедастичности:

1)оценки коэф по-прежнему останутся несмещенными и линейными 2)оценки будут неэффективн

3)дисперсия рассчитывается со смещением 4)выводы ненадежны, неверн заключения

Методы определения гетероск-графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфелра-Квандта.наиболее простой метод – графич.анализ отклонений – по оси абсцисс отклад значения х(либо линейный комбинации объясняющей переменной), а по оси ординат – отклонения или их квадраты.Если все отклонения нах внутри полосы постоянной ширины, паралл оси абсцисс, то это говорит о незав-ти дисперсий от значений х и их постоянстве – гомоскедатичность.Если набл-ся некотор изменения в соотношениях м/у значениями х и квадратами отклонений(лин, гиперболич зав-ть) то-гетероск.

Методы смягчения проблемы гетероскедастичности:

Метод взвешенных наименьших квадратов (МВНК).Устранить гетероск, разделив каждое наблюдаемое значение на соответсвующее ему значение среднего квадрат отклонения.тогда при оценке к-тов регрессии набл-я с меньшими дисперсиями отклонений будут более значимыми, чем набл-я с большими дисперсиями отклон.

В некот случаях для устранения гетероск надо изм-ть спецификацию модели.

Графич. представления поведения остаточного члена позволяет проанализировать наличие автокорреляции и гетероскедастичности, может быть обнаружена неправильная спецификация ур-ия.

По оси абсцисс – значения объясняющей переменной X (либо линейной комбинации объясняющей переменной), по оси ординат – отклонения (либо их квадраты)

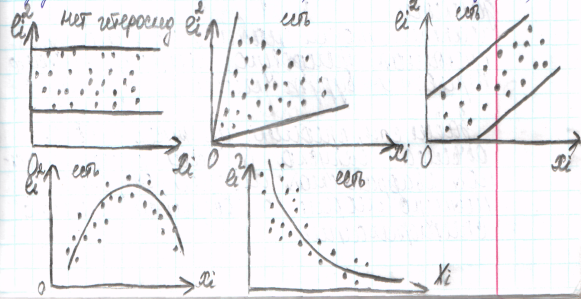
Методы смягчения проблемы гетероскедастичности:

Метод взвешенных наименьших квадратов (ВНК).

Устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответсвующее ему значение среднего квадрат отклонения.

16. Временные ряды и их классификация

Ряд динамики – ряд последовательно расположенных статистич-х показателей, изменение кот-х имеет определенную тенденцию развития изучаемого явления.

Временной ряд – последоват-ть наблюдений некоторого признака (случ-й величины y) в последоват-ные моменты времени.

Отдельные наблюдения наз. уровнями ряда,кот-ые обозначаются yt (t=1,2,…,n),где n-число уровней. Последовательно расположенные во времени числовые показатели характер-ют уровни состояния или изменения явления или процесса. Классификация ВР:1)в зависим-и от показателя времени ВР бывают моментные,т.е. на опред. дату, и интервальные, т.е. за опред. период 2) по форме представления уровни во ВР м.б. представлены абсолютными, средними и относительными величинами 3)по расстоянию между уровнями ВР подраздел-ся на ряды с равностоящими и неравностоящими уровнями по времени. 4)по содержанию ВР подразд-ют на стоящие из частных и агрегированных пок-лей. Несопоставимость уровней ВР: при построении ВР необходимо соблюдать опред.правила, нарушение кот-ых приводит к несопоставимости уровней ряда. Несопоставимость уровней ВР может возникать в результате неодинаковой полноты охвата объектов в том случае, если показатель представлен в различных единицах измерения, из-за сезонных явлений и т.д.Составляющие ВР: В общем виде при исследовании экономич. временного ряда у_t выделяют несколько составляющих.

Y_t=U_t+V_t+E_t , где U_t – тренд: плавно меняющаяся компонента,описыв чистое влияние долговременных факторов, т.е. длительную тенденцию изменен. признака, V_t – сезонная компонента, отраж повторяемость экономич процессов в течение не очень длительного периода, E_t – случайная компонента отражающая влияние не поддающихся счету и регистрации случайных факторов.

Аддитивная модель имеет вид Y_t=U_t+V_t+E_t

Мультипликативная имеет вид Y_t=U_t*V_t*E_t

Графич изображение составляющих временного ряда.