11. Проверка адекватности модели. Критерий Фишера.
После того как ур-ние регрессии построено выполняется проверка его адекватности и точности. Эти св-ва модели исслед-ся на основе анализа ряда остатков Еi (отклонений расчетных значений от фактич)
Уровень ряда
остатков
где i=1,2…n
Требования при кот модель считается адекватной: 1)уровни ряда остатков имеют случайный хар-р 2)математич ожидание уровней ряда остатков равно 0 3) дисперсия каждого отклонения одинакова для всех значений хi 4) значение уровней ряда остатков независимы др. от друга (отсутствие автокорреляции) 5) уровни ряда остатков распределения по нормальному закону.
t- критерий Стъюдента для оценки коэф регрессии
; 
где
,
-
стандартные отклонения свободного
члена и коэф регрессии. Определ по
формулам:
;
Где SE
–стандартное отклонение остатков
модели. Определ по формуле:
Расчетные знач
критерия сравнен с табличн
,
кот определяется при (n-k-1)
степенях свободы и соответствующем
уровне значимости.
Если расчетное значение больше табличного, то параметр признается значимым.
F-
критерий Фишера
Если при заданном уровне значимости расчетное значение критерия больше табличного, то модель считается значимой и надежной.
10.Множественная корреляция. Матрица парных линейных коэф корреляции, нахождение коэф множественной корреляции и коэф детерминации.
Ур-ние линейной множественной регрессии:
где
-параметры
модели(коэф регрессии);Е- случайная
величина
Матрица парных линейных коэф. корреляции
Коэф. множественной корреляции
,
где
-
определитель матрицы парных коэф
корреляции,
-
алгебраическое дополнение эл-та первой
строки и первого столбца(определитель
матрицы К , в кот вычеркнуты строка и
столбец, характеризующие связи независимых
переменных х с зависимыми переменными
у)
Коэф колеблется в пределах от 0 до1, чем ближе к 1, тем в большей степени учтены факторы, влияющие на результативный признак.
Коэф детерминации:
D=R2
Коэф детерминации определяет какая доля вариации признака у учтена в модели и обусловлена влиянием на него факторов включ в модель. Чем ближе R2 к единице, тем выше качество модели.
Критерий Фишера для множественной корреляции:
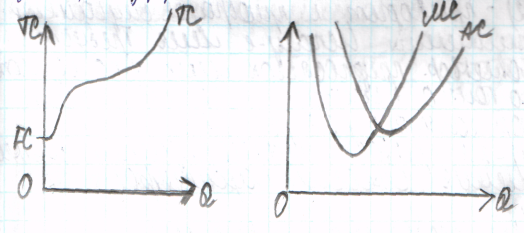
12. Нелинейные модели и их линеаризация. Обратная зависимость. Степенная и показательная модели.
Обратная модель
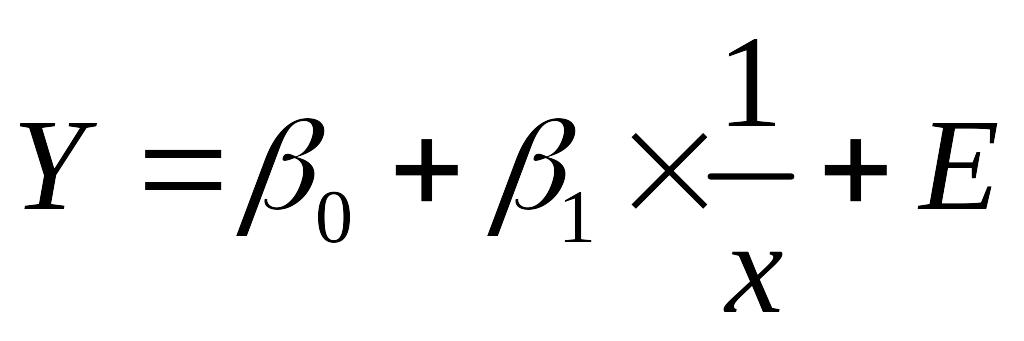
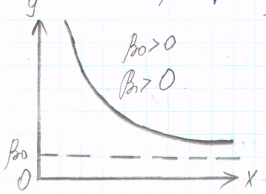
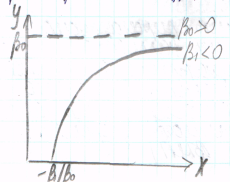
зависим между V выпус- зависим между доходом кривая Филипса, за-
ка(x) и средними фиксиро- (X) и спросом (Y) висим между уровн
ванными издержками (Y) безработицы(X) и
процентным изменен
зараб платы (Y)
Степенная
модель
- кубическая ф-ция – в микроэк-ке моделирует зависимость общих издержек (TC) от V выпуска (Q);
- квадратическая ф-ция – зависим между V выпуска (Q) и средними (AC) либо предельными (MC) издержками
Показательная
модель
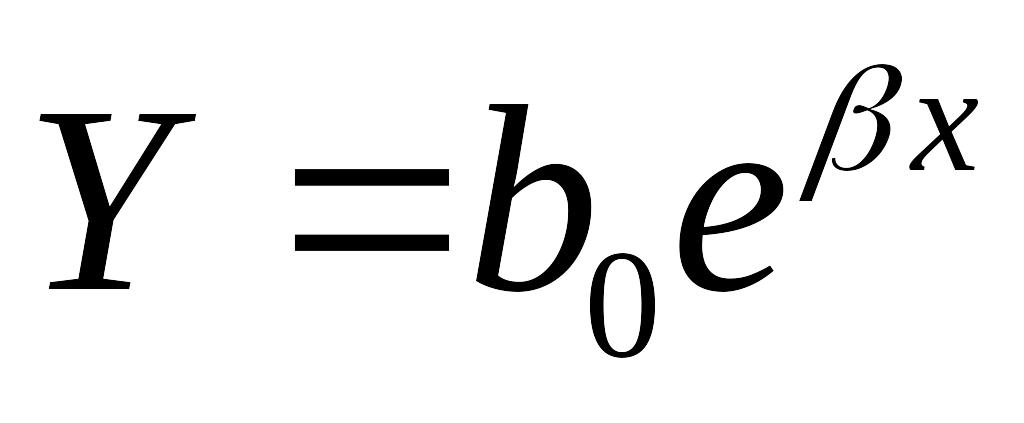
путем логарифмирования сводится сводится к логарифм-линейной модели:
