31.Временные параметры сетевого графика
Временные параметры работ:
Ранний срок
начала работы(i;j)
Ранний срок
окончания работы(i;j)
Поздний срок
окончания работы
(i;j)
Поздний срок
начала работы
(i;j)
Полный резерв времени работы –это максимально возможный запас времени, на который можно отсрочить начало работы или увеличить продолжительность её выполнения
Независимый(свободный) резерв времени работы – это запас времени, которым можно располагать при выполнении данной работы
Частный резерв
времени работы первого вида
Частный резерв времени работы второго вида
32.Модели управления запасами. Основные понятия.Основная модель управления запасами
Совокупность временно неиспользованных экономич рес-сов наз запасами предприятия (сырье, готовую продукцию и т.д.) Если требуются детали, а их нет на складе, то пр-во сможет остановиться. Если запасы увеличить, то возрастает стоимость их хранения. Задача УЗ - выбор целесообразного решения.
Кол-во товара, поставленного на склад наз размером партии.
График изменения запаса Q от времени t.
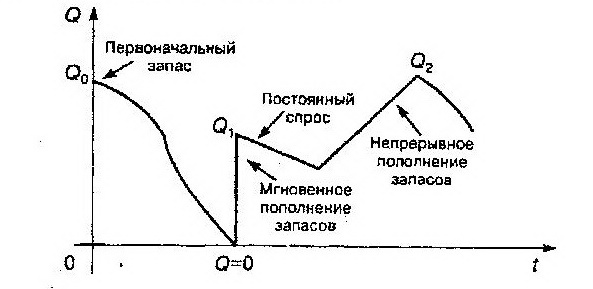
Q –изделия одного вида. Q=0 –дефицит
Математич модель, применяемая для УЗ должна учитыв издержки: 1)организационные связанные с оформлением и доставкой; 2)издержки содержания запасов-связаны с хранением (изделия могут портиться, устаревать и их кол-во уменьшаться), 3)издержки связанные с дефицитом (денежн. штраф, ухудшен бизнеса в будущем, потеря потребителей.)
Основная модель УЗ График изменения запасов
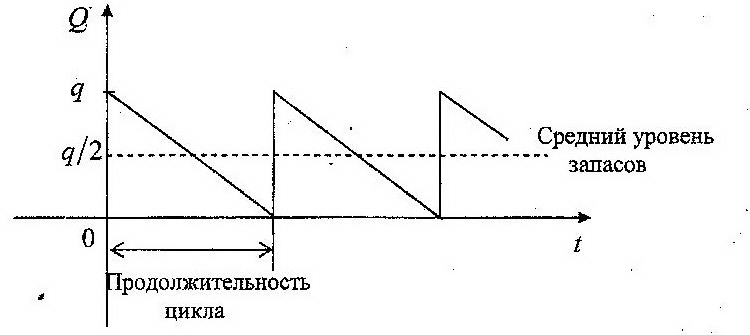
Величина |
Обознач |
Ед измерения |
Интенсивность спроса Организацион. издержки Стоимость товара Издержки содерж.запасов
Размер партии |
V K S h
q |
Ед товара в год Рубл за поставку Рублей Рубл за ед товара в год Ед товара в 1ой партии |
Чтобы удовлетворить годовой спрос V при размере поставки q необх V/q поставок за год . Средний уровень запасов q/2.
Ур-ие издержек
где С1-организацион издержки,С2-стоимость товара,С3-издержки содерж запасов.
Найдем
минимум: dC/dq=-KV/
+h/2=0,
- оптимальный
размер партии.
Неоптимальный размер приводит к увелич издержек
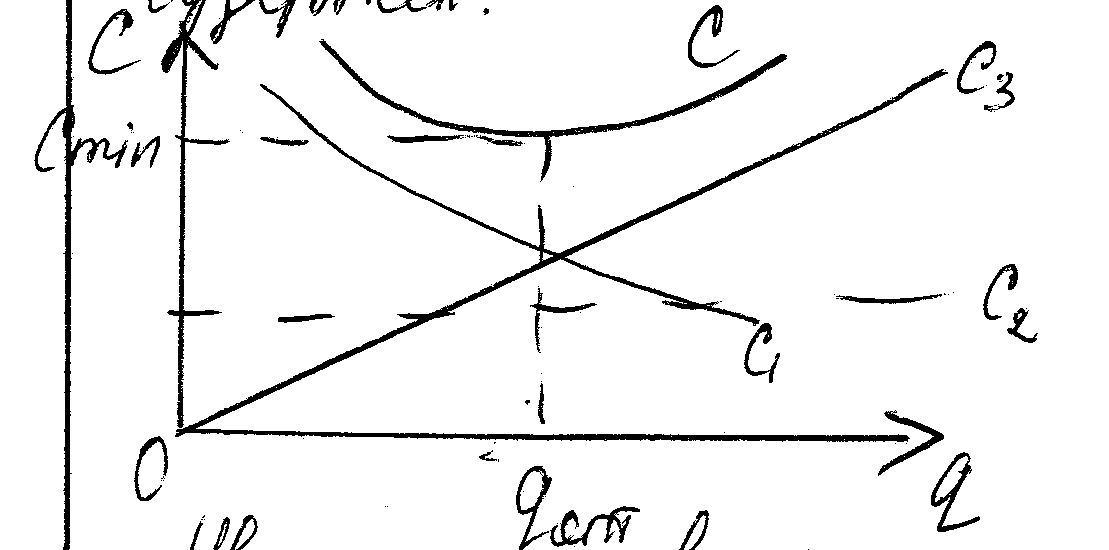
Увелич q
ведет к снижению
.
увелич
пропорц h/2.
34. Цель изучения смо, основные элементы. Классификация смо.
Цель изучения СМО-взять под контроль хар-ки обслуживающих сис-м установить зависимость м/у числом обслуживающих ед. и кол-вом обслуживания.
СМО применяется:
При поступлении сырья на скад и со склада
Обработке деталей на одном оборудовании
Организации наладки и ремонта оборудования
Определении численности обслуживающих отделов предпр.
Процесс работы СМО-случайный . Случайный процесс наз марковским, если его хар-ки зависят только от его состояния, а не от того , когда и как пришла сис-ма в это состояние.
Основными элементами СМО явл источники заявок, их входящий поток, каналы обслуживания и выходящий поток.
В зависимости от хар-ра формирования очереди различают:
1)сис-мы с отказами
2)сис-мы с неограниченным ожиданием
3)сис-мы смешанного типа
По числу каналов СМО делятся на одноканальные и многоканальные.
В зависимости от расположения источника требований разомкнутые (источники заявок вне сис-мы) и замкнутые (источники в сис-ме)
35. Ур-ние Колмогорова.Финальные вероятн. состояний СМО.
В этих ДУ неизвестные
ф-ции – вероятн. состояний сис-мы.
Вероятн. перехода из i-го
состоян. в j-е
за малый промежуток t
будет
где
-плотность
вероятности перехода (интенсивность
потока).
Пусть возможн.
состоян. сис-мы можно перечислить,
переход из одного в др происходит
мгновенно, вероятн. переходов
-вероятн.
нахождения сис-мы в i-ом
состоянии в момент t.
Найдем вероятн.,что в момент t+
t
сис-ма будет в состоян. S1
Вероятность, что сис-ма уже в этом
состоянии и за
t
оно не изменилось.р1(t)р11
Т.к. р11=1-р12-р13,
р1(t)*(
1-р12-р13)
S
2 S
1 р2(t)*р21
Сис-ма
может оказаться в S1
при переходе в него из любого иного
состояния с вероятностью
p2(t)р21+р3(t)р31
p1(t+ t)=p1(t)+p2(t)p21+p3(t)p31-p1(t)(p12+p13)
Выражаем вероятн.
через интен-ть:
Делим на
t
и переходим к пределу
Финансовые вероятности состояния СМО.
Решение задачи коши СДУ приводит к ф-циям времени РS (t)
Современем ф-ции сис-мы СМО переходит в стационарный режим с постоян. знан-и ф-ций Lim РS (t) =const=ps , s=0,R
Они называются финансовыми вероятностями
Полагая в СДУ
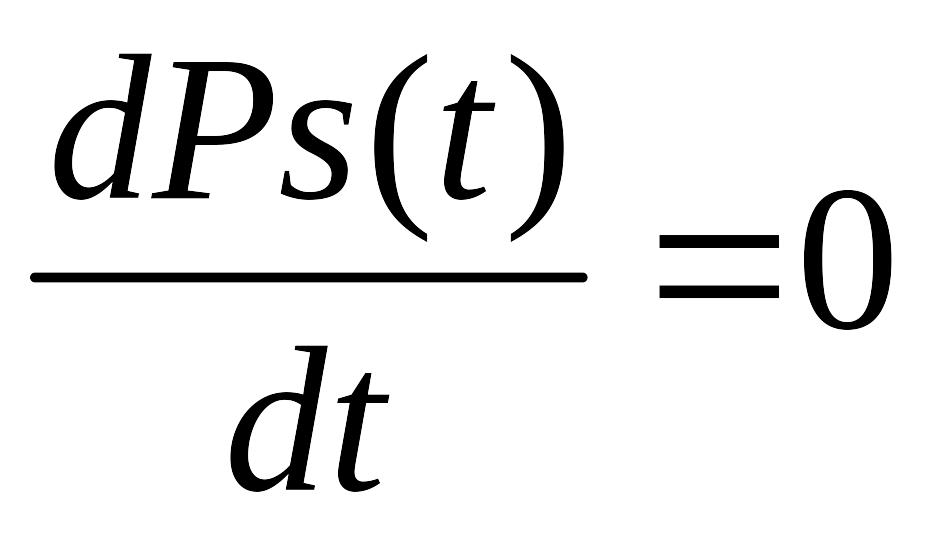
Получаем для их определения сис-му алгебраических ур-ний
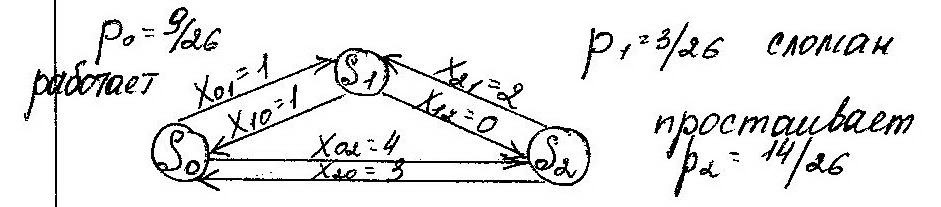
С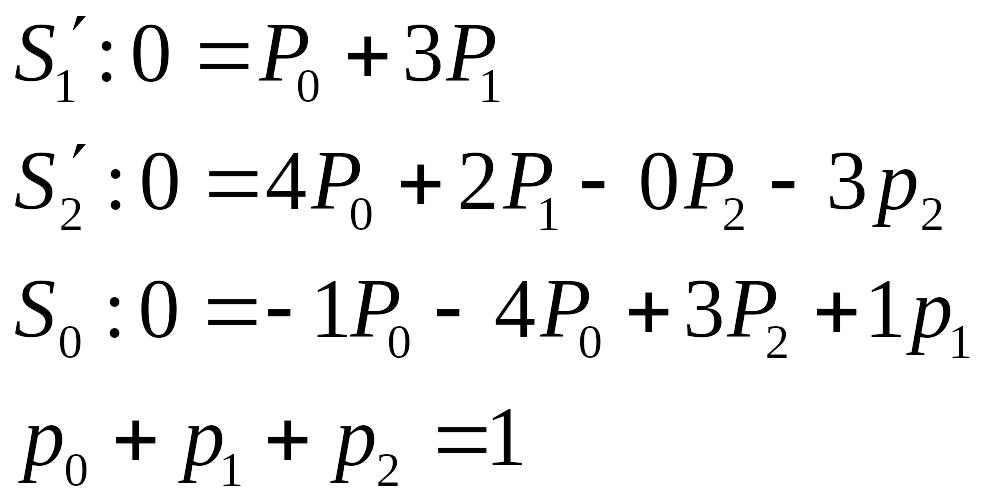
вероятн. Р1
=3/26 –оборуд. сломано,
Р2 =14/26-простаивает