- •4.Осн задачи и этапы коррел-регр анализа.Спецификация ур-я регрессии.Схема анализа зав-тей
- •5,6.)Парная линейная регрессия. Оценка коэф регрессии. Коэф эластичности. Метод наименьших квадратов
- •7.Предпосылки мнк (условия Гаусса-Маркова)
- •8.) Парная корреляция. Нахождение линейного коэффициента корреляции и парного коэффициента детерминации. Проверка значимости коэффициента корреляции.
- •9.Модель множественной линейной регрессии
- •10.Матрица коэффициентов парной регрессии. Коэффициент множественной корреляции. Коэффициент детерминации.
- •11. Проверка адекватности модели. Критерий Фишера.
- •10.Множественная корреляция. Матрица парных линейных коэф корреляции, нахождение коэф множественной корреляции и коэф детерминации.
- •12. Нелинейные модели и их линеаризация. Обратная зависимость. Степенная и показательная модели.
- •13. Мультиколлинеарность, ее последствия и причины возникновения.
- •1 4. Автокорреляция, ее основные причины и последствия.
- •15. Гетероскедатичность.Графический анализ отклонений.
- •16. Временные ряды и их классификация
- •17.Стационарный врем.Ряд
- •19. Системы одновременных уравнений
- •20. Идентификация модели. Необходимое и достаточное условие
- •21 Задачи и этапы эмм
- •22.Виды критериев оптимальности предп в соврем условиях
- •23. Понятие о методе межотраслевого баланса.
- •24. Стоимостный моб.
- •24.Смоб
- •25.Экономико-математическая модель моб
- •26. Матричные игры с нулевой суммой. Решение матричных игр в чистых стратегиях.
- •27. Решение матричных игр в смешанных стратегиях.
- •28.Игры с природой. Решение статистических игр при известных вероятностях состояний природы (критерии Байеса, Лапласа )
- •29.Вальда,Гурвица,Сэвиджа
- •29. Матрица рисков. Критерий Сэвиджа.
- •30. Элементы сетевого планирования. Основные понятия.
- •31.Временные параметры сетевого графика
- •32.Модели управления запасами. Основные понятия.Основная модель управления запасами
- •34. Цель изучения смо, основные элементы. Классификация смо.
- •36. Смо с отказами
29.Вальда,Гурвица,Сэвиджа
1.Махмin-ный критерий Вальда.
Согласно этому критерию рекомендуется применять маxмin-ную стратегию, она находится из условия
α=![]()
Критерий пессимистический, полагается что природа будет действовать наихудшим для игрока образом
2.Критерий максимума - оптимистический критерий. Считается, что природа наиболее благоприятна для игрока А и оптимальная стратегия находится из условия
m=![]()
3.Критерий Гурвица – рекомендует выбирать стратегии, определ. по формуле:
S=![]()
![]()
![]()
![]() )
)![]() }i=1;m
j=1;n
aij-элемент
платежной матрицы,
}i=1;m
j=1;n
aij-элемент
платежной матрицы,
![]() [0;1]-степень оптимизма
[0;1]-степень оптимизма
Критерий поддерживается некоторой промежуточной позицией, кот. учитывает возможность как наихудшего, так и наилучшего поведения природы. При =1 этот критерий превращается в критерий Вальда. При =0 получается критерий максимума, выбираем из опыта или субъективных соображений.
4.Критерий Сэвиджа. Суть состоит в выборе такой стратегии, кот. не позволяет допустить чрезмерно высокие потери. Этот критерий также как и критерий Вальда является критерием крайнего пессимизма, но пессимизм здесь понимается иначе. Тут рекомендуется всячески избегать большого риска. Согласно этому критерию выбирается стратегия, при которой в наихудших условиях величина риска принимает наименьшее значение, т. е.
r=![]() r
r![]() -элемент
матрицы рисков.
-элемент
матрицы рисков.
Пример: Создается ателье для ремонта телевизоров. Поток заявок на ремонт -2,4,6 и 8 тыс заявок. Прибыль от ремонта 1 телевизора – 9 денежных ед, потери вызванные отказом в ремонте-5ден. ед., убытки от простоя -6 ден.ед. Дать рекомендации о мощности создаваемого ателье.
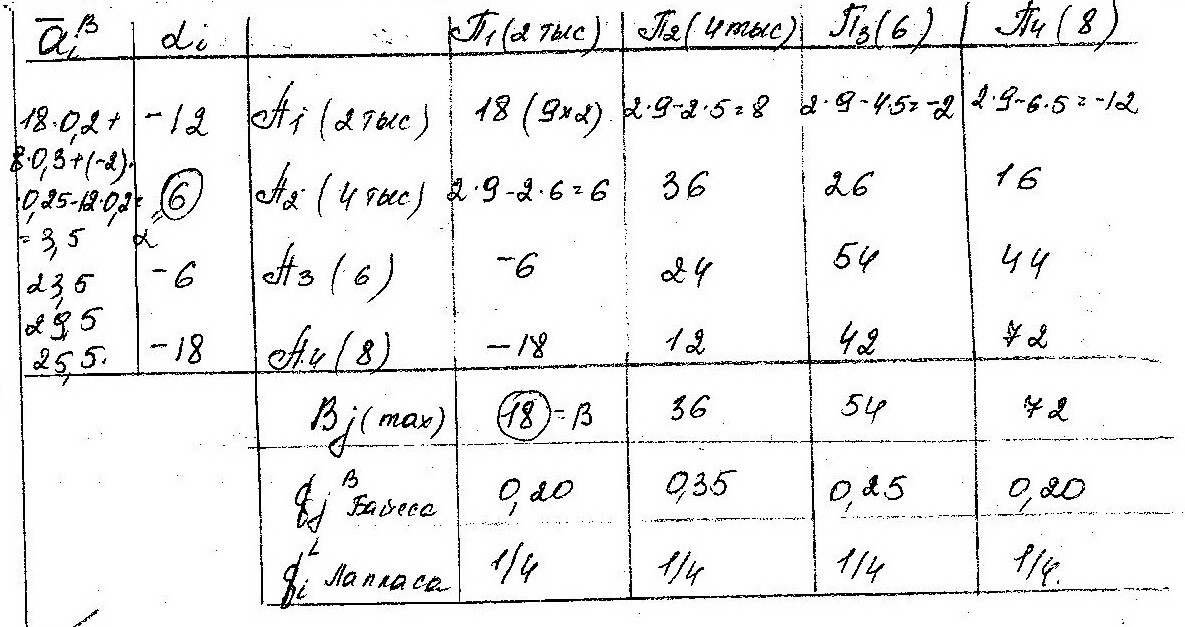
29. Матрица рисков. Критерий Сэвиджа.
Критерий Сэвиджа (крайнего пессимизма) – выбирать стратегию , при котор минимиз-ся величина максим риска. В области смешанных стратегий критерий Сэвиджа рекомендует выбирать стратегию р*, при которой максимум значений среднего риска минимиз-ся.

Оптимальной по Сэвиджу будет А3.
![]()
30. Элементы сетевого планирования. Основные понятия.
Сетевая модель – графич. изображение плана выполнения комплекса работ, состоящие из линий (работ) и узлов (событий), котор отражают взаимосвязь операций.
Работа – активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению рез-та.
Событие – это рез-т выполнения одной или нескольких предшествующих работ.
Фиктивная работа - связь между событиями, не требующая затарт времени и ресурсов.
Путь – непрерывная последовательность работ и событий.
Критичечкий путь – путь, не имеющий резервов, включ самые напряженные работы (критические).
Правила построения сетевых графиков.
Прежде чем представить проект сетевым графиком, необходимо составить перечень работ, оценить продолжительность каждой работы и установить последовательность работ, т.е. точно определить, какие работы обязательно должны быть закончены, чтобы могла начаться любая из работ, входящих в проект
При построении сетевых графиков следует соблюдать определенные правила:
В сетевых графиках не должно быть тупиков, т.е. событий из кот не выходит ни одна работа(за исключ. завершающего)
в сетевых графиках не должно быть и событий (кроме исходного), которым не предшествует хотя бы одна работа
при построении графиков нельзя допускать, чтобы 2 смежных события были связаны двумя или большим кол-вом работ
если для выполнения одной из работ необходимо получ рез-тов всех работ, входящих в предшествующее для нее событие, а для др работы достаточно получ рез-т только одной или нескольких из этих работ, то должно быть дополнительно введено новое событие, отраж рез-ы только этих последних работ, а также фиктивная работа, связывающая новое событие с прежним. Например работы а3 и а4.
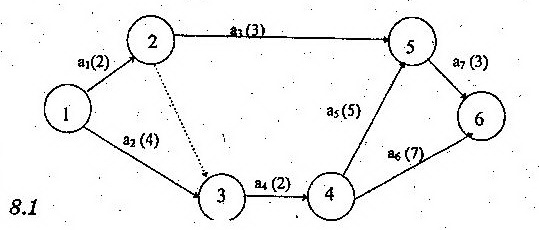
Основной – продолж критического пути:
1.Прямой подход (с исходного события до завершающего), определяем ранний срок наступления каждого события;
2.Обратный проход (с завершающего события до исходного), вычисл-ся поздний срок наступления событий.
Прямой:
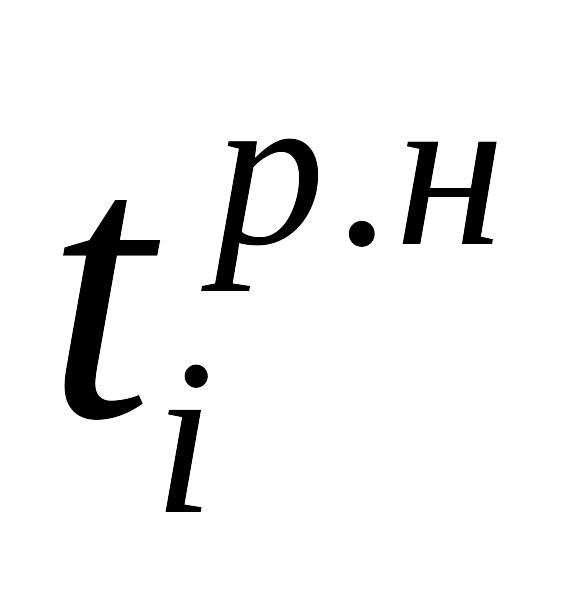 -
ранний срок начала всех операций,
выходящих из события i;
-
ранний срок начала всех операций,
выходящих из события i;
![]() - ранний срок начала
всех операций, входящих в j;
- ранний срок начала
всех операций, входящих в j;
![]() - продолжительность
операции (i,j);
- продолжительность
операции (i,j);
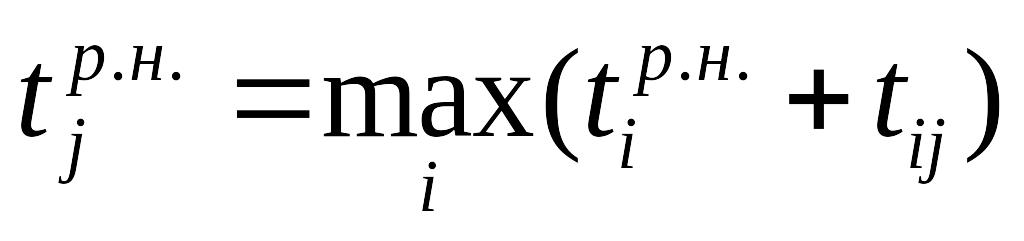 для всех (i,j).
для всех (i,j).
Обратный:
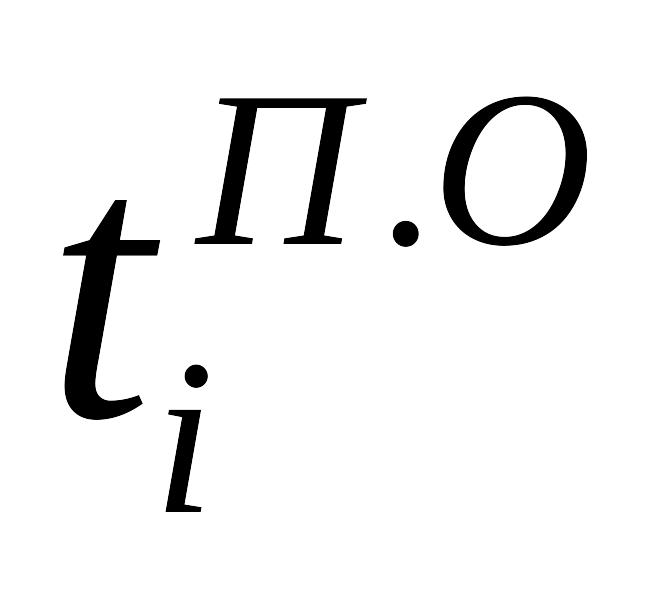 - поздний срок
окончания всех операций, входящих в i;
- поздний срок
окончания всех операций, входящих в i;
![]() - отправная точка
обратного прохода.
- отправная точка
обратного прохода.
Для всех операций (I,j)