26. Матричные игры с нулевой суммой. Решение матричных игр в чистых стратегиях.

Игрок А располагает m чистыми стратегиями (А₁,…,А_m), игрок В- n (В₁,…,В_n). Паре Аi и Вj соотв число а_ij – выигрыш игрока А за счет В (проигрыш В) . При а_ij<0 А платит В сумму а_ij. Если игра состоит из личных ходов, то выбор пары чистых стратегий определяет исход игры. Если в игре используют случайные ходы, то ее исход определяется средним значением выигрыша (т.е. математич. ожиданием)

Платежная матрица игры: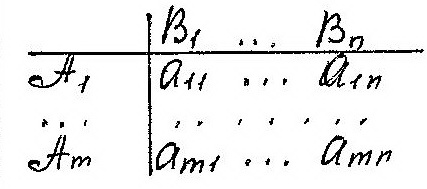

Решение матричных игр в чистых стратегиях.

Стратегию игрока А наз оптимальной, если при ее применении выигрыш А не уменьшается, какими бы стратегиями не пользовался В.

Оптимальной для В наз стратегию, при кот проигрыш В не увеличивался.

Принцип осторожности- игрок, считая партнера разумным, полагая, что соперник не упустит возможность использовать промахи в своих интересах. Игрок А для каждой Аi найдет min значение выигрыша: а_i=min а_ij

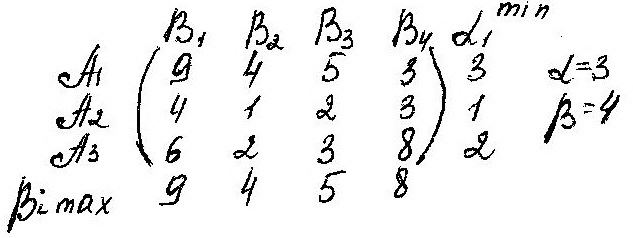
-нижняя чистая цена игры (максимин)-минимальный выигрыш игрока А, правильно применяющего свои чистые стратегии. Для В минимальная стратегия где -верхняя чистая цена игры(минимакс)-maх проигрыша В при правильном выборе стратегии.

Если , то игра имеет седловую точку и чистую цену игры.

27. Решение матричных игр в смешанных стратегиях.

Игрокам надо так выбирать стратегии, чтобы партнер не догадался о них

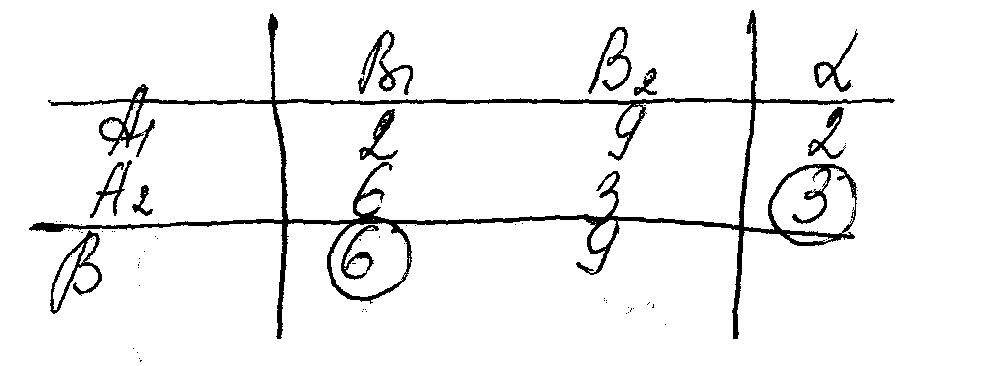
р1,……рm – вероятности, с котор А использует стратегии А1,…..Аm: .

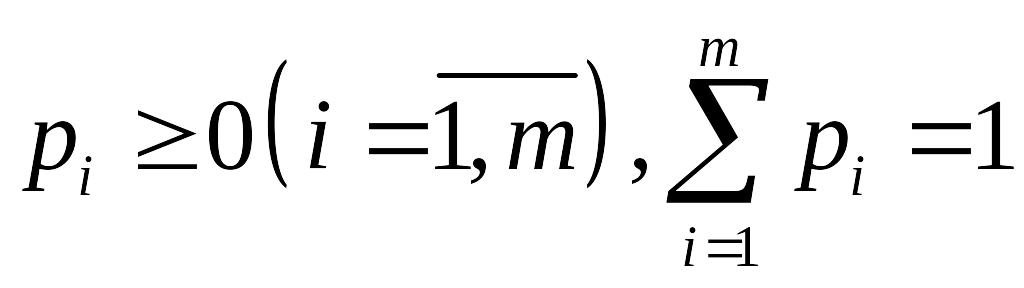р=(р1…..рm) – смешанная стратегия. Чистая стратегия – частный случай смешанной р=(0,…..,1,….0).

q=(q1;…..;qn) – смешанная стратегия B.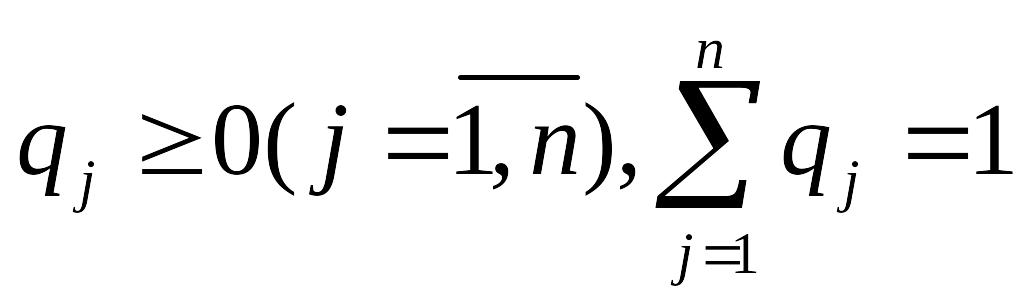

Игроки выбир-т стратегии случайно и независимо друг от друга, вероятность выбора комбинации .

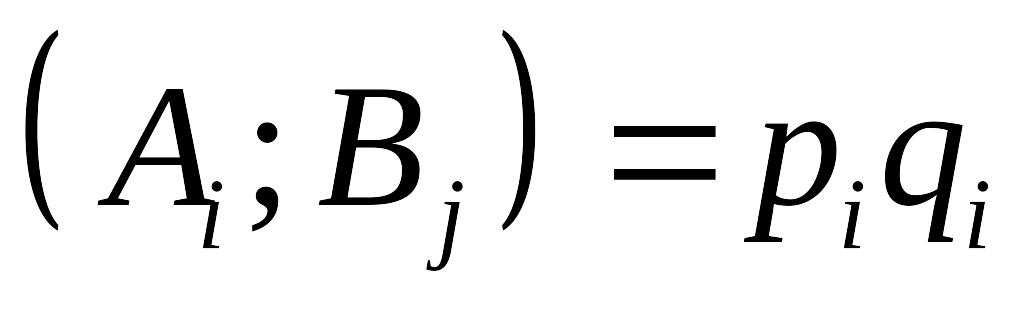Средняя величина выйгрыша

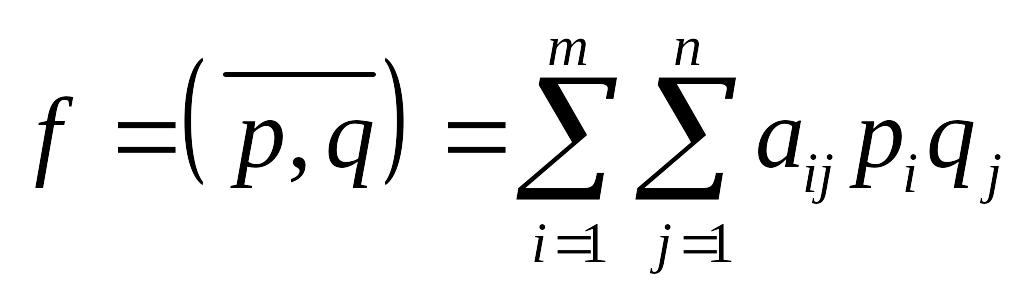
Решение можно упростить, выявив доминир-ее стратегий.

Если 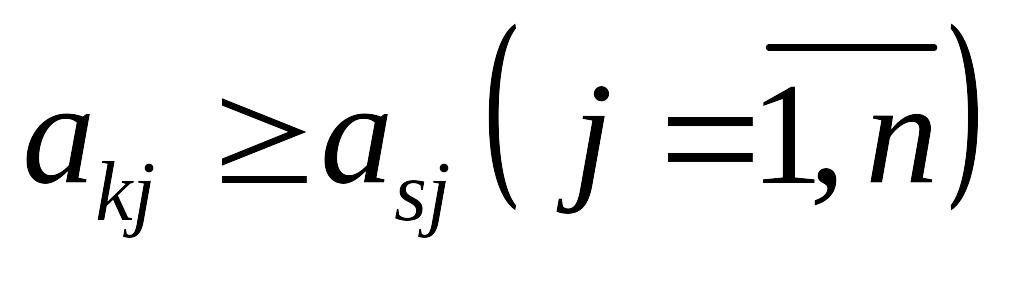,то выйгрыш А при больше, чем при . Аналогично 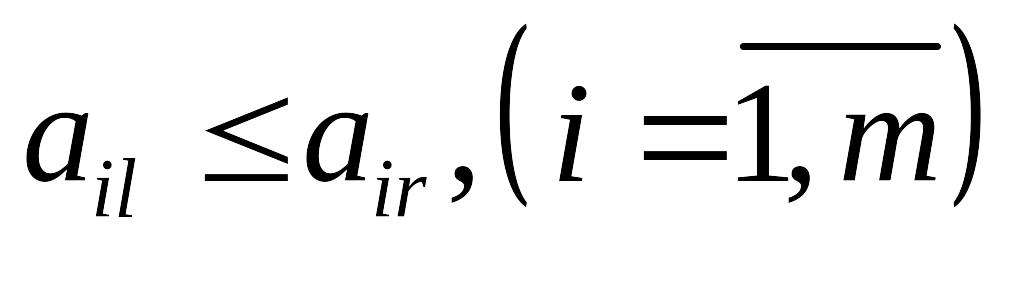. В невыгодно применять . Стратегия доминирует над стратегией .

28.Игры с природой. Решение статистических игр при известных вероятностях состояний природы (критерии Байеса, Лапласа )

Сознательный игрок А (статистик), заинтерес-ый в исходе против участника, безразличн к рез-ту (природы П). При решении достаточно найти рекомендации для А, природа в рекомендациях не нужд-ся. Обычно известны возможные состоянии природы, а иногда и их вероятности. Эти вероятности наз-т априорными. Отбрасывать состояния природы нельзя. Риском статистика наз-ся разность между максим выйгрышем, котор он мог бы получить, зная, что природой будет реализовано состояние и выйгрышем, котор он получит использ стратегию .

, где - максим элемент j-го столбца.

Решение оцен-т с различных позиций. Если известны вероятности состояний природы:

Среднее значение выйгрыша

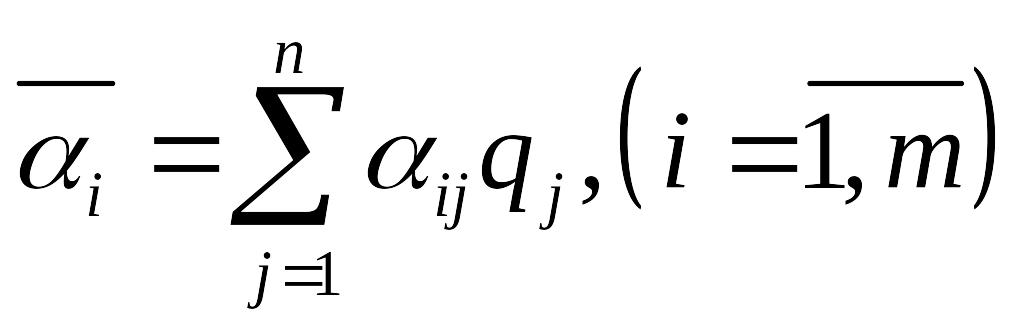
Среднее значение риска .

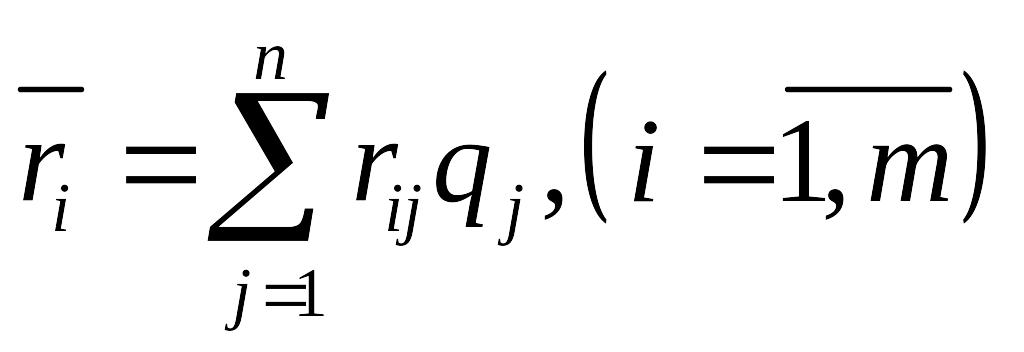В качестве оптимальной по критерию Байеса приним-ся стратегия , максимиз-щая средний выйгрыш.

Если статистик считает состояния природы в равной мере возможными, то q1=…..=qn=1/n – принцип недостаточного основания Лапласа.

28. Под стат. игрой или игрой с природой мы будем понимать парную матричную игру, в кот. 1 игрок заинтересован в наиболее выгодном для себя исходе игры, а второй игрок-природа (П), совершенно безразличен к результату игры. Предположим, что в игре с природой сознательный игрок А м. Использовать m чистых стратегий: A₁,A₂,…..A_m, а 2 игрок П м. реализовать n различных состояний: П₁,П₂…П_n. Игроку А м.б. известны вероятности q₁,q₂….q_n, с кот. природа реализует свои состояния, но он может и не знать их. Действуя против природы, игрок А м. реализовать как свои чистые стратегии A_i, так и смешанные. Если игрок А в состоянии оценить некоторой величиной а_ij последствия применения каждой своей чистой стратегии A_i при любом состоянии природы П_j, то игру м. задать платежной матрицей.

А_m*n=

Игры с природой явл-ся частным случаем матр. игр.

При упрощении платежной матрицы отбрасывать те или иные состояния природы нельзя, т.к. она м. реализовать любое состояние независимо от того выгодно оно или нет. Решение достаточно найти только для игрока А поскольку природа наши рекомендации воспринять не может. Смешанные стратегии приобретают смысл только при многократном повторении игры.

Решение статистич. игры: 1) упростить платежную матрицу. Отбрасывать стратегии природы нельзя (столбики на месте) 2) оценить выигрыш при различных игровых ситуациях(критерий Байеса, Вальда, Гурвица, Сэвиджа. 3) построить и исследовать матрицу риска 4)сделать вывод о выборе наилучшей стратегии.

Матрица рисков Сэвиджа

Построение матрицы рисков. Риском r_ij игрока А, когда он пользуется своей чистой стратегией А_i при состоянии природы П_j наз. разность м/у min-ым выигрышем, кот. он м. бы получить, если бы точно знал, что природой б. реализовано именно состояние П_j и тем выигрышем, кот он реально получит, используя стратегию A_i, не зная какое же состояние реализует природа.

r_ij=_j-a_ij>=0, _j=maxa_ij, i=1,m

i Где В_j=max a_ij – максимальный элемент j-го столбца платежной матрицы. Элементы матрицы рисков, соответствующие стратегиям А_i и П_j характеризуют общую благоприятность или не благоприятность для игрока А отдельных состояний природы.

критерий Байеса:Критерий, основанный на известных вероятностях условий. Пусть известны вероятности q_j состояний природы П , j=1;n.Тогда пользуемся критерием Байеса, в соответствии с кот. Оптимальная считается чистая стратегия A , при которой максимизируется средний выигрыш =

Принцип недостаточного основания Лапласа:

Если объективные оценки состояния природы получить невозможно, но вероятности природы могут быть оценены субъективно на основе принципа недостаточного основания Лапласа, согласно которому все состояния природы полагаются равновероятностными, т.е.q₁=q₂=…….=q_n= и оптимальной считают стратегию А_i, обеспечивающую максимальное среднее значение выигрыша =