24.Смоб

Виды стоимостного МОБ: 1).Отчетный баланс. На основе отчетного стоимостного баланса проверяется в какой мере затраты компенсированы доходами. 2).Плановый баланс. Позволяет сопоставить планируемые затраты с возможными доходами.Осн понятия СМОБ

Единая система цен. При разработке стоимостного баланса могут быть использованы следующие цены: 1).фактические цены производителя. Они показывают, сколько стоит продукт в месте его производства(не учитываются транспортно-заготовительные расходы). В ценах производителей рекомендуется строить плановые стоимостные баланса. 2). фактические цены конечного потребления. Они включают затраты, связанные с реализацией продукции и отражают стоимость продукта в месте его потребления. Отчетные стоимостные балансы строятся в ценах конечного потребления. 3).Расчетные цены. Они соответствуют действительным издержкам производства продукции каждой отрасли.

Стоимостной МОБ состоит из 4-х квадрантов, каждый из которых хар-ет отдельные стороны или процессы расширенного производства. Важнейшей частью стоимостного МОБ является I квадрант, поскольку он хар-ет межотраслевые связи в сфере материального производства. I квадрант – таблица размерности nxn, наименование строк и столбцов которой соответствует чистым технологическим отраслям материального производства. В строках и столбцах в одинаковом порядке перечислены одни и те же отрасли материального производства (табл.1).

Обозначения: Xi – валовой выпуск продукции i-ой отрасли за рассматриваемый промежуток времени, xij – межотраслевые потоки продукции от i-ой отрасли к j-ой отрасли, xii- главная диагональ МОБ, ее элементы стоят на пересечении строк и столбцов одноименных отраслей и хар-ют внутреннее потребление каждой отраслью своей же продукции, Yi – объем продукции отрасли i, потребляемый в непроизводственной сфере, - конечное потребление. Рассм. МОБ для 3-х отраслей народного хоз-ва.

Строки I квадранта отражают межотраслевые поставки сырья, материалов, топлива и т.д. отраслям материального производства в денежном выражении.

Столбцы I квадранта стоимостного баланса хар-ют состав материальных затрат в денежном выражении на производство продукции отдельных отраслей.

Во II квадранте МОБ хар-ет конечное потребление каждого вида продукции.

25.Экономико-математическая модель моб

Основу ЭМ модели МОБ составляет матрица, содерж-ая коэф-ты прямых затрат на производство единицы продукции.

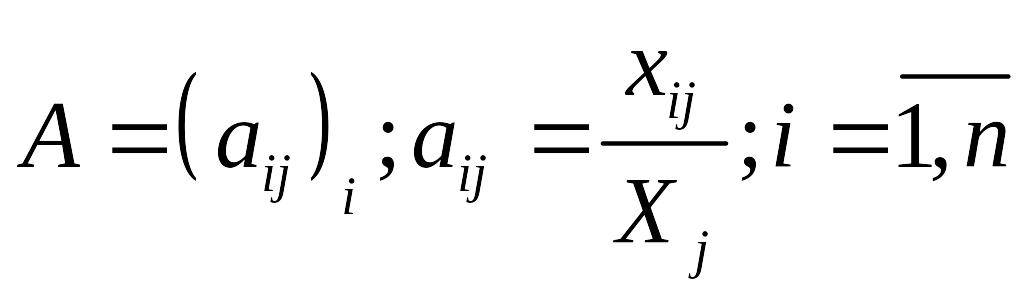где - какое кол-во продукции i-ой отрасли необходимо, учитывая только прямые затраты для произ-ва ед-цы продукции j-ой отрасли.

Межотраслевые потоки опред-ся по формуле:

Т.к. по строкам МОБ – распред-ее продукции на произв-ве и конечное потребление, то сис-ма ур-ий баланса: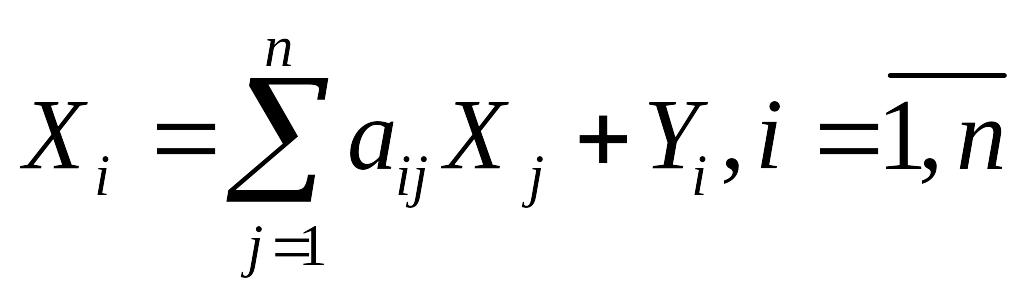

или МОБ в матричной форме: X = A*X + Y (6), где Х-вектор-столбец валовой продукции, У-вектор-столбец конечной продукции. А=( a_ij )_nxn – матрица коэф-тов прямых материальных затрат.

С учётом эк-кого смысла задачи, все коэф-ты матрицы А и компоненты векторов Х и У должны быть неотрицательны.

Различают математические модели отчётного и прогнозного МОБ. Модель отчётного МОБ Xj = + Zj , j=1,n и Xi = +Yi , i =1,n. Мат модель прогнозного МОБ Xi = a_ij*X_j + Y_i , i=1,n или в матричной форме: X = A*X + Y модели прогнозного МОБ -модель Леонтьева, модель “затраты-выпуск”).

Расчёты, выполняемые по модели:

1.Задавая в модели величины валовой продукции каждой отрасли (Х_i), можно определить объем конечной продукции в каждой отрасли Yi:Y = (E – A)*X (7)

2.Задавая величины конечной продукции всех отраслей (Yi) можно определить величины валовой продукции каждой отрасли (Xi):

X = (E –A)^-1*Y (8)

3.Для ряда отраслей задавая величины валовой продукции, а для всех остальных отраслей - объемы конечной продукции можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. Е- единичная матрица, (E –A)^-1 – обратная матрица.

Матрица коэф-тов полных затрат.

Обозначим обратную матрицу (E – A)^-1 через В, тогда модель затраты-выпуск можно записать в виде X = B*Y

Матрица В=(b_ij)_nxn есть матрица коэф-тов полных затрат. Коэф-ты полных затрат пок-т сколько нужно произвести прод i-й отрасли для выпуска в сферутконечного исп-ния единицы прод j-й отрасли.

Коэф-ты полных затрат можно применять тогда, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объёмов конечной прод-ции всех отраслей. дельтаXi = b_ij*дельтаY_i; i=1,n, где дельтаXi, дельтаY_i - изменения (приросты) величин валовой и конечной продукции соответственно.