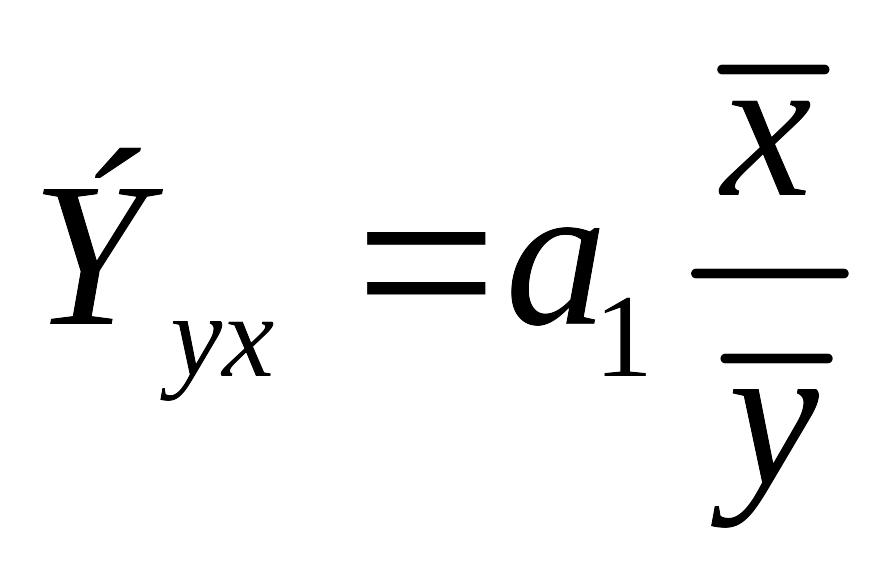1.Цель, задачи эконометрики. Понятия эконометрической модели и эконометрической моделирования.Э.-наука, предметом изучения кот явл. колич. выражение взаимосвязей эконом. явлений.

Цель эконометрики- разработка способов моделир. и колич. анализа реальн. эконом. объектов.

Задачи эконометрики: 1)Спецификация модели(построен. эконометрич. моделей для эмперич. анализа) 2)Параметризация модели (оценка параметров построен. модели) 3)Верификация модели(проверка качества параметров модели и самой модели в целом) 4)Прогнозирование модели(составление прогноза и рекомендаций для конкретн. эконом. явлений по рез-там эконометрич. моделир)

Общий вид эконометрической модели: y=f(x)+Е

где у – наблюд. знач. зависим. переменной, f(х) – объясненная часть, кот зависит от знач объясняющих перемен (факторов), Е – случайная составляющая (ошибка)

Эконом-ая модель-совок-ть матем-их соотнош-ий м/у входными и выходными переменными изучаемого экономического явления.Экон-ое моделиров-е- исследование эконометрич явлений и процессов посредством их эконометрич моделей.

2. Этапы эконометрического моделирования. Классы эконометрической моделей. Типы данных в эконометрике.Этапы эконометрического моделирования:

1. Постановочный (сформулир. проблема)

2. Априорный (основные экзоген. и эндоген. переменные определяем)

3. Параметризация (выбираем вид зависимости)

4. Информационный (собираем инф-цию)

5. Идентификация модели (находим модель)

6. Верификация модели (проверка модели)

Классы эконометрических моделей:

1.Регрессионные модели с одним ур-нием. Результативный признак представлен в виде ф-ции от факторных признаков y=f(x)+ɛ=f(X1,X2,X3)+ ɛ.у-наблюдаемое значение эндогенной переменной, f(X)-объясненная часть, кот зависит от экзогенных переменных, ɛ-случ составляющая(ошибка).Пример – модель зав-ти цены от объема поставки.

2.Сис-мы одновременных ур-ний. Состоят из тождеств и регрессион ур-ний, в кот вместе с факторн признаками включены результативные из др. ур-ний сис-мы. Т.е. одни и те же перемен одновременно рассматрив как зависим перемен в одних ур-ниях и независим в др. Например:модель спроса и предлож. Кейнсианская модель формир доходов.

3.Модели временных рядов. Результативн признак явл ф-цией переменной времени или перемен относящ к др. моментам времени. Например: модели описыв зависим от времени: тренда, сезонности, тренда и сезонности.

Типы данных:- пространственные. Об однотипных объектах в 1 и тот же момент времени (объем произ-ва предприятий региона).- временные. Данные об 1ом и том же объекте в различные мом-ты времени(индекс потребительских цен).

3. Корреляционная зависимость и ее ,виды. Классификация связи в зависимости от направления действия и количества признаков.Корреляционная зависимость – связь, при котор каждому значению независимой переменной соотв-т определенное математич. ожидание.Завис-ти от напр-я дей-я:связь прямая(с увелич-ем значимости фактор-го признака происх.увеличение результат-го приз-ка)обратная(с увели-ем факто-го приз-ка происх.уменьш-ие результ-го приз-ка.Типы зависимостей между явлениями и их признаками: функциональная (каждому значению независимой переменной X соот-т точно определенное значение зависимой переменной Y); статистическая (это связь, при которой каждому значению независимой переменной X соот-т множество значений зависимой переменной Y и изменение которой носит случ хар-р); корреляционная –частный случай статистич(это связь, при которой каждому значению переменной X соот-т определен матем ожидание (ср.значение), при изменении одной из величин, изменяется средн значение другой.

Виды корреляц зависимости: парная (связь между двумя признаками (резулт Y и факторный X или двумя факторн); частная (зависимость м/у результ и одним факторн признаками или м/у двумя факторными при фиксированном значении др факторн признаков);множественная (зависимость м/д результ признаком и 2 или более фаторн признаками, вкл в исследование).

Теснота связи кол-но выражается коэф-том корелляции.

Виды связи в зависимости от кол-ва признаков: однофакторн (связь м/д 1 факторн признаком и 1 результативн признаком при абстрагировании от влияния других); многофакторн (связь м/д несколькими факторн и 1 результативн признаком).

4.Осн задачи и этапы коррел-регр анализа.Спецификация ур-я регрессии.Схема анализа зав-тей

Задачи корреляцион-регрессион анализа: установление формы корреляцион связи, т.е. вида функции регрессии (линейн, квадратичн, показательн); оценка тесноты корреляцион связи Y и X; оценка неизвестных параметров регрессион модели, проверка гипотез об их значимости и адекватности модели рассматриваемому эконом объекту).

Перед корреляционно-регрессионным анализом стоят следующие основные задачи:

1.установление формы корреляционной связи, т. е. установление вида функции регрессии (линейная, квадратичная, показательная и т. д.);

2.оценка тесноты корреляционной связи У и X (степени рассеяния значений СВ У около Ух). Большое рассеяние означает слабую зависимость У от X либо вообще ее отсутствие. Малое рассеяние указывает на существование достаточно сильной зависимости У отХ;

3.оценка неизвестных параметров регрессионной модели, проверка гипотез об их значимости и адекватности модели рассматриваемому экономическому объекту.

1А+Б18 (Этапы корреляционно-регрессионного анализа). Корреляционно-регрессионный анализ проводится поэтапно в определенной логической последовательности:

1.предварительный анализ явлений и выяснение причин возникновения взаимосвязей между признаками, характеризующими эти явления, разделение признаков на факторные и результативные, выбор наиболее существенных признаков;

2.предварительная оценка формы уравнения регрессии и определение уравнения регрессии, расчет теоретически ожидаемых значений результативного признака, оценка тесноты связи между признаками, включенными в регрессионную модель.

3.общая оценка качества модели, отсев несущественных (или включение дополнительных) факторов, построение исправленной модели;

4.статистическая оценка достоверности параметров уравнения регрессии, построение доверительных границ для теоретически ожидаемых по уравнению регрессии значений функции и получение практических выводов из проведенного анализа.

Отметим, что в корреляционном анализе изучается в основном сила (теснота) корреляционной зависимости, а в регрессионном анализе - ее форма.

Проблема спецификации

Опред. Выбор формулы связи переменных называется спецификацией уравнения регрессии. В случае парной регрессии выбор формулы обычно осуществляется по графическому изображению реальных статистических данных.

Виды ошибок спецификации.

1. Отбрасывание значимой переменной.

Оценки, получен. по такому урав-ию являются смещенными и несостоятельными, интервальные оценки и рез-ты проверки гипотез будут ненадежными.

2. Добавление незначимой переменной.

Оценки остаются, как правило, несмещенными и состоятельными. Однако их точность уменьшится, т.е. оценки становятся неэффективными, что отразится на их устойчивости.

3. Выбор неправильной функциональной формы.

Приводит либо к получ. смещенных оценок, либо к ухудшению статистич. св-в оценок коэф-тов регрессии и других показателей качества ур-ия. Прогнозные качества модели очень низки.

5,6.)Парная линейная регрессия. Оценка коэф регрессии. Коэф эластичности. Метод наименьших квадратов

У р-ние регрессии или модель связи соц-эконом явлений, выражается ф-цией.

где к–число факторных признаков

Парная регрессия- Множественная регрессия (хар-ет

(хар-ет связь м/у результ связь м/у результ и 2-мя и более

и Факторн признаками) факторными признаками)

Ур-ние линенейной парной регрессии – это у_х=а₀+а₁х_i+Е_i, где а₀, а₁-параметры модели_; Е_i-случ величина; а₀-свободный член регрессион ур-ния. а₁-показывает на кокую величину в среднем измен-ся результ признак у, если переменная х увелич на ед. измерения.

Знак при коэф регрессии показыв направление связи при а₁>0-связь прямая; а₁<0-связь обратная.

Е_i-отражает факт,что изменение у будет неточно описывать изменение х, т.к. присутствуют др. факты, не учтенные в данной модели.

Оценка параметров модели осущ методом наименьших квадратов.

;

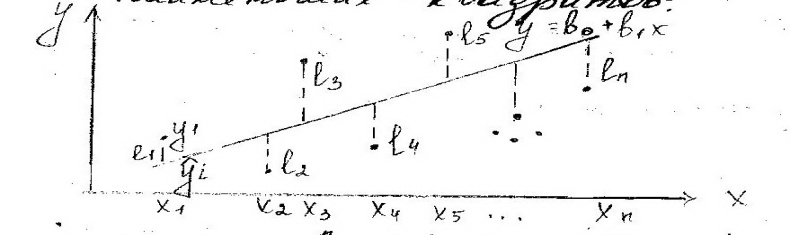
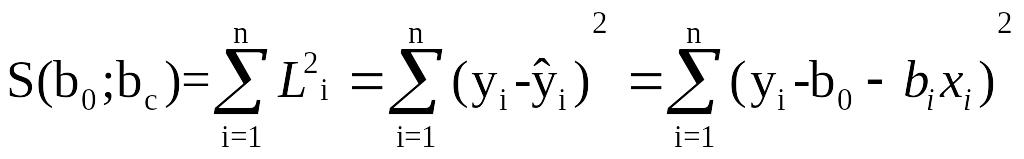
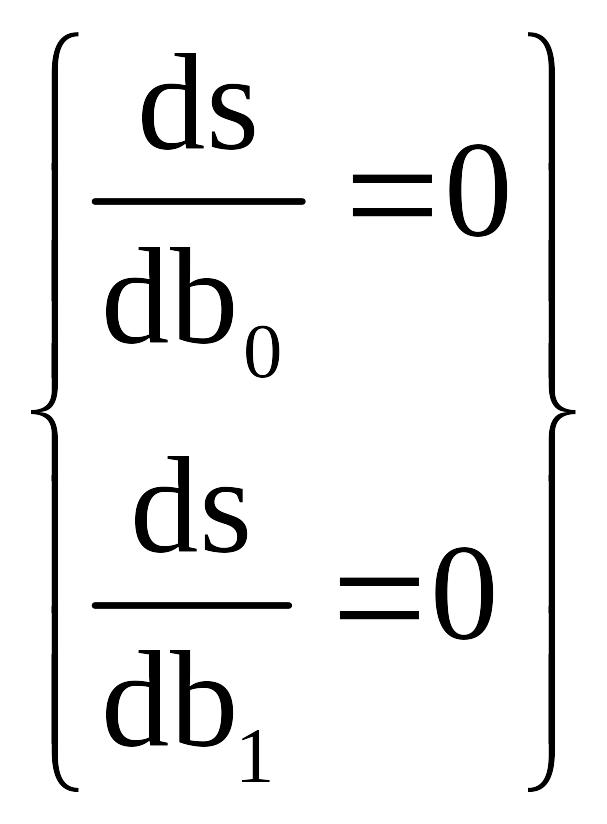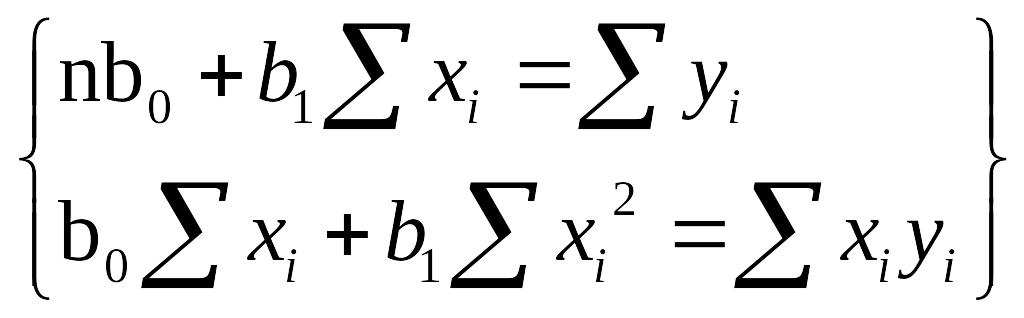
Необходимо, чтобы выполнялся ряд предпосылок относит случ отклонения

Коэф эластичности показ на сколько % изменился результ признак у, при изменен факторного признака х на 1 %