6 Рівняння Парка - Горєва

Для того, щоб позбутися періодичних коефіцієнтів у системі диференційних рівнянь (5.1), (5.2) електричної рівноваги напруг ОС та ОР синхронної машини, необхідно за допомогою перетворення координат замінити дійсні змінні новими змінними. Довільну трифазну систему змінних h_А, h_В, h_С можна зобразити у вигляді проекцій узагальненого вектора на осі трифазної системи координат (рисунок 6.1), якщо виконується умова

. (6.1)

Нехай узагальнений вектор обертається з кутовою швидкістю ротора СГ . Тоді його проекції на осі А,В,С (рисунок 6.2)

(6.2)

де - кут між узагальненим вектором та магнітною віссю фази А.

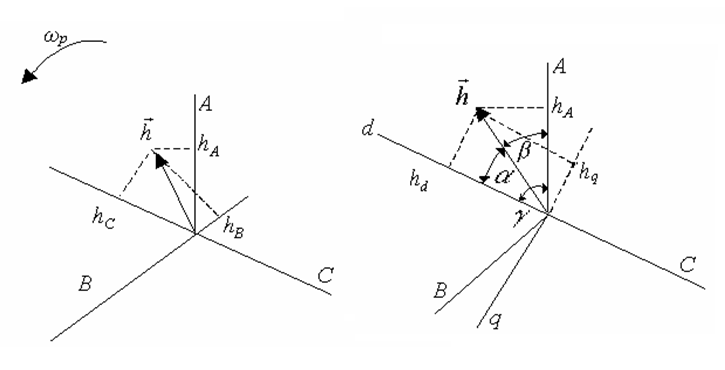
Рисунок 6.1 - Узагальнений Рисунок 6.2- Перетворення

вектор координат з використанням

узагальненого вектора

Введемо взаємно ортогональну систему координатних осей d,q так, щоб вектор нерухомо лежав у їх площині (сама система d,q обертається з кутовою швидкістю , тобто жорстко зчеплена з ротором СГ, причому вісь d збігається з поздовжньою віссю ротора машини).

У цьому випадку проекції узагальненого вектора на осі d,q будуть сталими в часі

(6.3)

де - кут між вектором та поздовжньою віссю d.

Перехід від системи фазних координат до нової обертової системи координат здійснюється за формулами

(6.4)

де γ – кут між віссю d і віссю фази А,

. (6.5)

Оскільки нами прийняте припущення про симетрію фаз ОС СГ, то нульова складова . Застосувавши формули переходу ( 6.4 ) до параметрів режиму фази А ОС, одержимо

(6.6)

Підставимо (6.6) в перше рівняння системи (5.1) і після диференціювання та прирівнювання коефіцієнтів при однакових функціях кута γ одержимо в операторній формі

(6.7)

При досліджені перехідних процесів СГ зручно оперувати не кутом γ, який визначає положення ротора відносно статора, а кутовою швидкістю обертання ротора

. (6.8)

Підставивши ( 6.8 ) в ( 6.7 ) та доповнивши отриману систему рівнянням ( 5.2 ), маємо

(6.9)

Система диференційних рівнянь (6.9), записана в системі відносних одиниць, дістала назву рівнянь Парка – Горєва. Тут складові - ЕРС трансформації. Вони виникають під час зміни відповідного потокозчеплення. В усталеному режимі ЕРС трансформації відсутні. Складові та дістали назву ЕРС обертання, їх значення пропорційні кутовій швидкості обертання ротора СГ . Ці ЕРС встановлюють електромеханічний зв’язок між статором і ротором, оскільки характеризують перетворення електричної енергії в механічну та навпаки. Складові та - відповідно відображають теплові втрати енергії в обмотках СГ.

Рівнянням Парка – Горєва ( 6.9 ) можна дати наступну фізичну інтерпретацію. Три нерухомі фазні ОС можна замінити двома еквівалентними контурами, що обертаються разом з ротором (рисунок 6.3) і по яких протікають струми і_d та і_q . Магнітні осі контурів спрямовані вздовж осей d і q. По осі d СГ має два контури - W_d ОС і W_f ОР, об`єднані потоком взаємоіндукції По осі q розміщений один контур W_q. Оскільки осі d і q взаємно ортогональні, то магнітні зв'язки між контурами, що розташовані по цих осях, відсутні. У системі відносних одиниць потокозчеплення фаз

(6.10)

Тут х_d , х_q – відповідно синхронні індуктивні опори СГ по осях d і q;

х_аd – індуктивний опір реакції якоря по повздовжній осі d (опір взаємозв'язку між ОС і ОР).

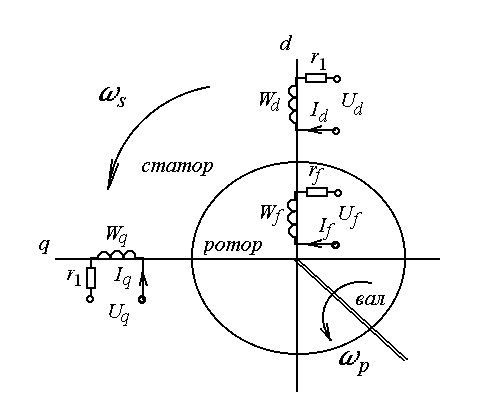
Рисунок 6.3 - Схема СГ без демпферних обмоток в обертових осях d,q

Якщо, знехтувати ЕРС трансформації та активним опором r₁ ОС, то для сталої кутової швидкості обертання ротора СГ одержимо спрощені рівняння Парка – Горєва, в яких фігурують діючі значення змінних величин

(6.11)

Спрощені рівняння Парка-Горєва використовують для розрахунку надперехідного струму КЗ, а також для експрес-аналізу стійкості режимів енергосистем.