5 Диференційні рівняння електромагнітного стану явнополюсного синхронного генератора у фазній системі координат

Точний розрахунок струмів КЗ в електричних системах неможливий без детального аналізу перехідних процесів, що протікають в їх джерелах – синхронних генераторах ( СГ ).

Розглянемо математичну модель явнополюсного СГ, який працює паралельно з системою нескінченої потужності (рисунок 5.1)

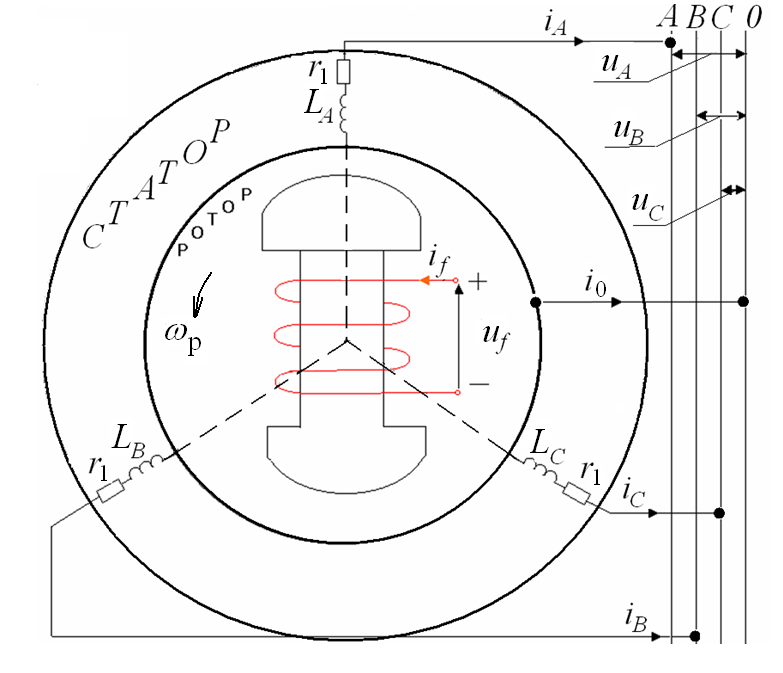
Рисунок 5.1 – Принципова схема явнополюсного СГ

При створенні математичної моделі приймаємо такі припущення:

• на роторі СГ розміщена лише одна обмотка збудження;

• електричні та магнітні кола СГ лінійні (відсутнє насичення магнітних шляхів);

• розподіл магніторушійних сил у повітряному проміжку СГ синусоїдний (обмотки є “синусні”);

• фазні обмотки СГ симетричні;

• відсутні втрати в магнітній системі СГ.

Запишемо диференційні рівняння електричної рівноваги в операторній формі для обмотки статора (ОС)

(.1)

Для обмотки ротора (ОР) аналогічно буде

(5.2)

де u_A, u_B, u_C , Ψ_A, Ψ_В, Ψ_С , i_А , i_В , i_C - відповідно напруги, повні потокозчеплення та струми фаз ОС;

u_f , Ψ_f , i_f - напруга, потокозчеплення та струм ОР ;

r₁, r_f - активні опори відповідно ОС та ОР,

p=d/dt – оператор диференціювання за часом.

Згідно з прийнятими припущеннями повні потокозчеплення обмотки є лінійними функціями відповідних струмів

(5.3)

де L_А , L_B , L_С , L_f - відповідно власні індуктивності фаз ОС та ОР ;

M_AB , M_BА , M_AС , M_СА , M_BС , M_СB - взаємні індуктивності між фазами ОС ;

M_Af , M_fA , M_Bf , M_fB , M_Cf , M_fC - взаємні індуктивності між фазами ОС та ОР.

У відповідності з принципом взаємності M_AB = M_BА, M_Af = M_fB і т.д.

Під час обертання неявнополюсного ротора змінюється величина повітряного проміжку машини, тобто магнітний опір на шляху силових ліній робочого поля. Це призводить до зміни магнітного потоку і пов`язаної з ним зміни індуктивностей СГ. Отже, всі власні та взаємні індуктивності машини (крім L_f) залежать від положення ротора відносно статора, тобто є функціями часу.

Закономірність зміни власних індуктивностей проаналізуємо на прикладі зміни індуктивності L_A. Положення ротора відносно статора будемо відстежувати за зміною кута  між віссю фази А статора та поздовжньою віссю d ротора СГ (рисунок 5.2).

. (5.4)

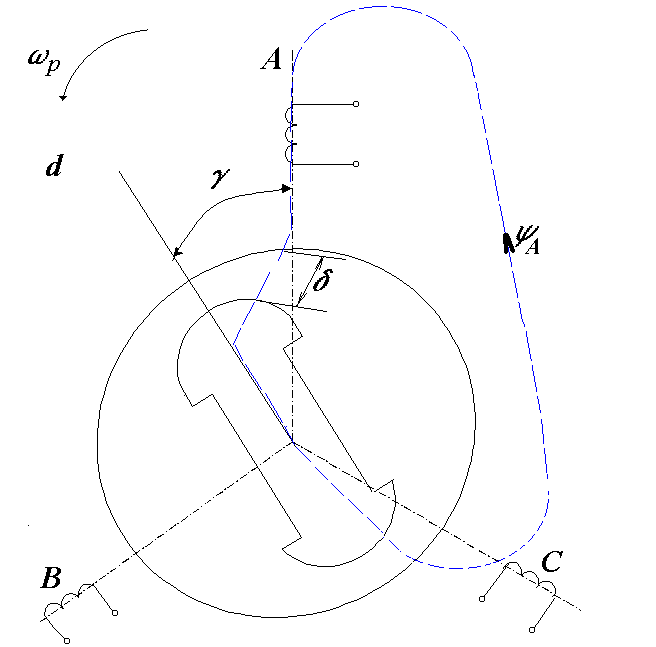
Рисунок 5.2 – До визначення власної індуктивності L_A

При сталій швидкості обертання ротора ω_P= const маємо

 = ₀ + ω_P t . (5.5)

Очевидно, що L_A є періодичною функцією кута , оскільки ця індуктивність є максимальною при значеннях кута  =0,,… (коли повітряний проміжок  є мінімальним) і мінімальною при значеннях . Отже залежність L_A() є періодичною парною функцією з періодом , яку можна розкласти в ряд Фурє

L_A = l₀ + l₂ cos 2 + l₄ cos 4 +… . (5.6)

Відсутність синусних функцій непарних гармонік пояснюється тим, що L_A є парною функцією кута , тобто не має значення, в який бік обертається ротор СГ. Згідно з припущенням про “синусність” обмоток СГ залишимо в (5.6) лише перші два члени розкладу

L_A  l₀ + l₂ cos 2 , (5.7)

де l₀,l₂ – відповідно середнє значення та амплітуда зміни індуктивності фази ОС

(5.8)

де – відповідно максимальна та мінімальна індуктивність фази ОС (рисунок 5.3).

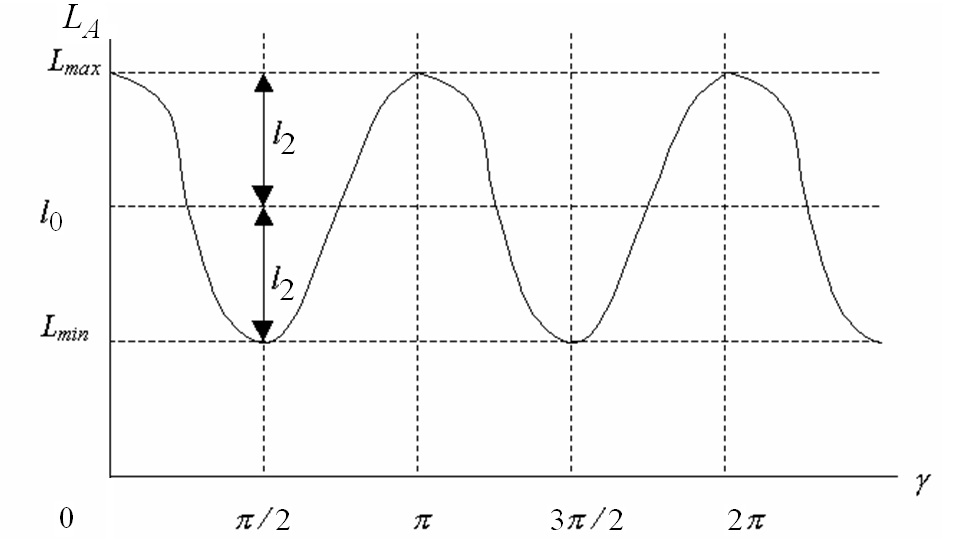
Рисунок 5.3 - Залежність власної індуктивності L_A від кута 

Остаточно одержимо аналітичні вирази для власних індуктивностей фаз ОС у вигляді

(5.9)

Аналогічно можна одержати взаємні індуктивності між ОС та ОР, які є періодичними функціями кута  (рисунки 5.4 та 5.5)

(5.10)

де m₀ ,m₂ – відповідно середнє значення та амплітуда зміни взаємної індуктивності між ОС та ОР.

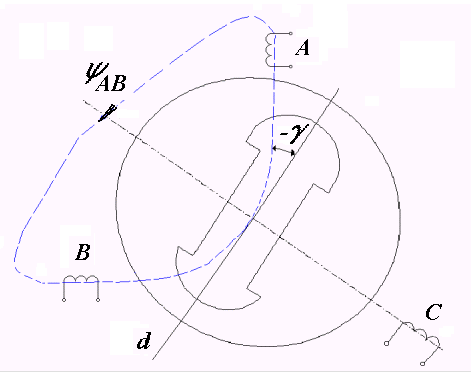
Рисунок 5.4 - До визначення взаємної індуктивності M_АВ

Очевидно, що , оскільки осі фаз ОС зміщені на кут . Слід також відзначити, що m₂=l₂.

Оскільки обмотка збудження, яка розміщена на роторі СГ, переміщується відносно статора, то взаємні індуктивності між ОС і ОР будуть періодично змінюватися, досягаючи максимального значення М_Аfd при суміщенні магнітних осей обмоток:

(5.11)

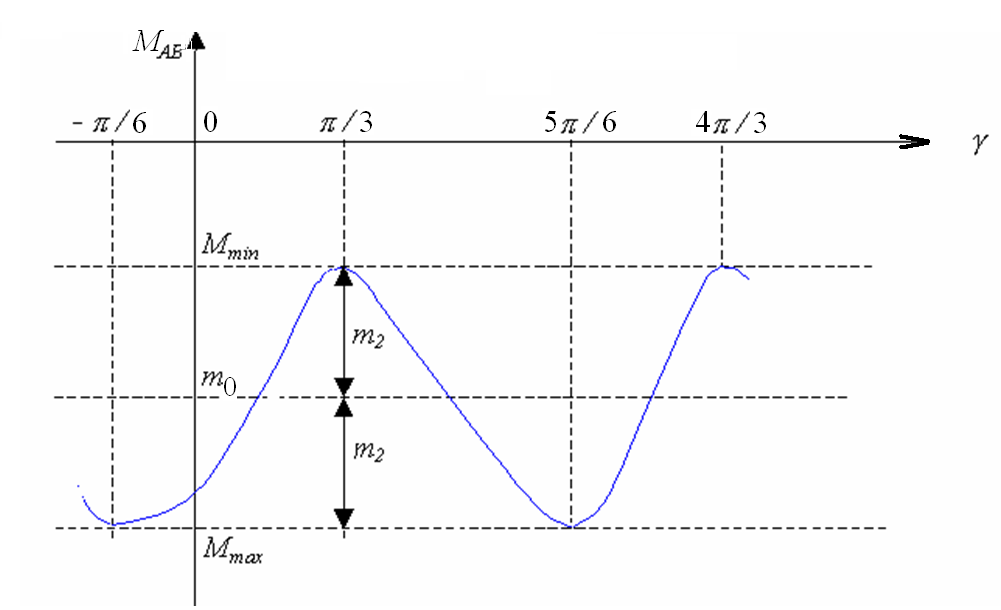
Рисунок 5.5 – Залежність взаємної індуктивності m_AB від кута 

Таким чином, взаємні та власні індуктивності СГ(крім індуктивності L_f) є гармонічними функціями кута повороту  ротора відносно статора, а отже і часу t. Згідно з (5.3) потокозчеплення обмоток СГ теж є складними функціями кута . Якщо підставити ці потокозчеплення в рівняння електричної рівноваги напруг (5.1),(5.2), то одержимо систему диференційних рівнянь з періодичними коефіцієнтами, розв`язок якої пов`язаний зі значними труднощами.