1.

Матрицей размера m× n называется прямоугольная таблица элементов некоторого множества (например, чисел или функций), имеющая m строк и n столбцов. Элементы, из которых составлена матрица, называются элементами матрицы.

Различают следующие матрицы:

1. Квадратная матрица – число строк совпадает с числом столбцов. 2. Матрица-столбец.

3. Матрица-строка. 4. Нулевая матрица – все элементы равны нулю.

5.Единичная матрица – на гл. диагонали расположены единицы, осталь-ные элементы равны нулю. 6.Диагональная матрица – на гл. диагонали расположены произвольные числа, остальные - нули.

7. Верхняя треугольная матрица – ниже главной диагонали расположены нули.

8. Нижняя треугольная матрица – выше главной диагонали расположены нули.

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число.

Для любых чисел a и b и матриц A и B выполняются равенства:

1. . 2. 3.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C.

Легко проверить, что сложение матриц подчиняется следующим законам:

1.коммутативному A+B=B+A 2.ассоциативному (A+B)+C=A+(B+C).

3.существованию нулевого элемента А+0 = А. 4.существованию обратного элемента А + (-А) =0.

2. Матрицей размера m× n называется прямоугольная таблица элементов некоторого множества (например, чисел или функций), имеющая m строк и n столбцов. Элементы, из которых составлена матрица, называются элементами матрицы.

Различают следующие матрицы:

1. Квадратная матрица – число строк совпадает с числом столбцов. 2. Матрица-столбец.

3. Матрица-строка. 4. Нулевая матрица – все элементы равны нулю.

5.Единичная матрица – на гл. диагонали расположены единицы, осталь-ные элементы равны нулю. 6.Диагональная матрица – на гл. диагонали расположены произвольные числа, остальные - нули.

7. Верхняя треугольная матрица – ниже главной диагонали расположены нули.

8. Нижняя треугольная матрица – выше главной диагонали расположены нули.

Две матрицы A_mxn  и B_mxn называются согласованными, если число столбцов матрицы А совпадает с числом строк матрицы В. Умножать можно только согласованные матрицы.

Произведением матрицы A_kxn на матрицу B_nxm  называется матрица C_kxm, у которой число строк k совпадает с числом строк матрицы А, а число столбцов m совпадает с числом столбцов матрицы В:

.

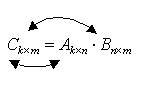Если матрицы А, В и С подходящих порядков, то справедливы следующие свойства операции умножения матриц.

1. ассоциативности умножения матриц . А*(В*С) = (А*В)*С

2.Два свойства дистрибутивности . (А+В)*С = А*С+В*С и А*(В+С) = А*В+А*С

3.В общем случае операция умножения матриц некоммутативна .А*В ≠В*А

4. А*Е =А или Е*А =А. 5.О* А =О, А*О = О.

3.

Перестановкой из n натуральных чисел называется любое их расположение и обозначается (a₁,a₂,... a_n).

Если в перестановке большее число стоит впереди меньшего, то два числа образуют инверсию. Число инверсий в перестановке(a₁,a₂,... a_n) обозначается k(a₁,a₂,... a_n). Если число инверсий в перестановке четное (нечетное), то перестановка четная (нечетная). Теорема 1. При перестановке местами двух чисел четность перестановки меняет-ся на противоположную.

4.

Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

.

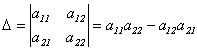
Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

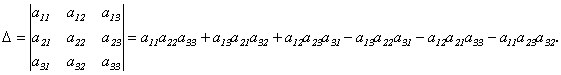
О пределителем n-го порядка квадратной матрицы А_{n x n} называется число, равное алгебраической сумме a_i1A_i1 + a_i2A_i2 +... +a_inA_in (1.12), где А_ij(j=1,2,...n) является определителями (n-1)-го порядка, полученными из исходного вычеркиванием i-й строки и j-го столбца и умножением на (-1)^i+j .

 Свойства определителей:

1.При транспонировании квадратной матрицы её определитель не меняется:

2.Общий множитель в строке можно выносить за знак определителя.

3.Если квадратная матрица -го порядка умножается на некоторое ненулевое число , то определитель полученной матрицы равен произведению определителя исходной матрицы на число в степени, равной порядку матриц.

4. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

5.Если две строки определителя поменять местами, то определитель поменяет знак.

6. Определитель с двумя равными строками равен нулю.

7.Определитель с двумя пропорциональными строками равен нулю.

8.Определитель, содержащий нулевую строку, равен нулю.

9.Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

10.Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

11.Определитель произведения матриц равен произведению определителей:

5.

Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.

Обозначение: a_ij - выбранный элемент определителя,M_ij - его минор.

Алгебраическим дополнением A_ij элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е. A=(-1)^i+jM_ij.

Разложение определителя

По элементам i-й строки:

По элементам j-го столбца:

6.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0.

Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Обратная матрица матрице А, обозначается через А^-1, так что В = А^-1 и вычисляется по

формуле     

,

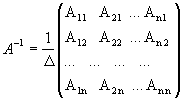где А _{i j} - алгебраические дополнения элементов a _{i j} матрицы A..

7.

Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля

rang A = K, если , M_k+1= 0 , M_k+2= 0,....

Приведём основные методы вычисления ранга матрицы.