II. Диа и парамагнетизм. Зависимость магнитной восприимчивости от температуры. Закон Кюри.
Для исследования магнитных свойств вещества из него изготавливают небольшой стерженек (или трубку, если жидкое) и наблюдают поведение вещества в сильном магнитном поле.
Если испытуемый стрженек помещен в поле, то действие поля на него сводится к определению ориентации его в этом поле:
а) если стерженек в однородном поле устанавливается поперек линий поля, а в неоднородном выталкивается в область слабого поля – диамагнетик.
|
Диамагнетики: Cu, Bi, Sb, Ag, Au, Pb, J, C, Hg, Si, Zn, S, H2O, N2, CO2, благородные газы и органические соединения. |
б) если стерженек в однородном поле устанавливается вдоль линий индукции поля , а в неоднородном также вдоль линий поля и втягивается в область более сильного поля парамагнетик.
|
К парамагнетикам относятся: Al, Mn, Cr, Sn, Pt, растворы солей железа, твердый и жидкий О2, воздух, органические соединения… |
Как же объяснить магнитные свойства веществ?
А. Парамагнетики.
а) |
Их свойства объясняются наличием у атомов магнитного момента . В отсутствие магнитного поля магнитные моменты атомов ориентированы беспорядочно (а). Во внешнем поле (б) на каждый атом действует пара сил и магнитные моменты атомов устанавливаются по полю и . При этом направление намагничения ( направлено от Sк N) оказывается параллельно . Объяснение парамагнетизма в точности совпадает с теорией поляризации диэлектриков. Отметим: теория парамагнетизма была развита Ланжевеном раньше теории диэлектриков и Дебай перенес эту теорию на диэлектрики. |
б |
)Парамагнитный эффект зависит от температуры, т.к. тепловое движение атомов или молекул нарушает ориентацию их магнитных моментов во внешнем магнитном поле. Для многих парамагнетиков зависимость изменения æ с температурой подчиняется закону:
– закон Кюри, (6)
где С – постоянная Кюри, зависит от рода вещества.
Температура Кюри Тк – температура, при которой ферромагнитные свойства исчезают совсем. Для различных веществ она различна:
Кобальт: 1150°С
Никель: 360°С.
При температурах выше температуры Кюри действует другой закон:
– закон Кюри-Вейсса (7)
Магнитная восприимчивость
Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом(намагниченностью) вещества и магнитным полем в этом веществе[1].
Определение
Магнитная восприимчивость определяется отношением намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. По своему смыслу восприимчивость является величиной безразмерной.
,
где 
—
намагниченность вещества под действием
магнитного поля, 
—
напряженность магнитного поля.
Иногда бывает полезно также ввести понятие удельной магнитной восприимчивости, равной восприимчивости единицы массывещества. В СИ удельная восприимчивость измеряется в обратных килограммах (кг−1). Аналогично, молярная магнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях (моль−1).
Магнитная проницаемость среды
Магнитная проницаемость
[править]
Материал из Википедии — свободной энциклопедии
Магнитная
проницаемость — физическая
величина,
коэффициент (зависящий от свойств
среды), характеризующий связь
между магнитной
индукцией 
и напряжённостью
магнитного поля 
в
веществе. Для разных сред этот коэффициент
различен, поэтому говорят о магнитной
проницаемости конкретной среды
(подразумевая ее состав, состояние,
температуру и т. д.).
Впервые встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») в 1881 году[1].
Обычно
обозначается греческой буквой 
.
Может быть как скаляром (у изотропных
веществ),
так и тензором (у анизотропных).
В общем связь соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как
и в общем случае здесь следует понимать как тензор, что в компонентной записи соответствует[2]:
Для изотропных веществ соотношение:
можно понимать в смысле умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру).
В системе СГС магнитная проницаемость — безразмерная величина, в Международной системе единиц (СИ) вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости:
,
где 
—
относительная, а
—
абсолютная проницаемость, 
— магнитная
постоянная (магнитная
проницаемость вакуума).
Нередко обозначение используется не так, как здесь, а именно для относительной магнитной проницаемости (при этом совпадает с таковым в СГС).
Размерность абсолютной магнитной проницаемости в СИ такая же, как размерность магнитной постоянной, то есть Гн/м илиН/А2.
Магнитная проницаемость связана с магнитной восприимчивостью χ следующим образом: в СИ:
в Гауссовой системе:
Вообще говоря магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля (а кроме того от температуры[3], давления итд).
Также зависит от характера изменения поля со временем, в частности, для синусоидального колебания поля — зависит от частоты этого колебания (в этом случае вводят комплексную магнитную проницаемость чтобы описать влияние среды на сдвиг фазы 'B' по отношению к 'H'). При достаточно низких частотах (небольшой быстроте изменения поля) ее можно обычно считать в этом смысле константой.
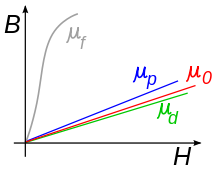
Схематический график зависимости 'B' от 'H' (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков(μf), парамагнетиков (μp), вакуума(μ0) идиамагнетиков (μd)
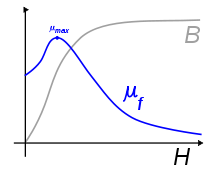
Кривая намагничивания дляферромагнетиков (и ферримагнетиков) и соответствующий ей график магнитной проницаемости
Магнитная проницаемость сильно зависит от величины поля для нелинейных сред (типичный пример — ферромагнетики, для которых характерен гистерезис). Для таких сред магнитная проницаемость как независящее от поля число может указываться приближенно, в рамках линеаризации[4].
Для парамагнетиков и диамагнетиков линейное приближение достаточно хорошо для широкого диапазона величин поля.
Теорема о циркуляции
Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил ее (см. ниже). Уравнение, представляющее собой содержание теоремы в этом обобщенном виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей - то есть в принципе вмагнитостатике - верна теорема в первоначальном виде, сформулированном Ампером и приведенном в статье первым; для общего случая правая часть должна быть дополнена членом с производной напряженности электрического поля по времени - см. ниже). Теорема гласит[1]:
Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции. |
Эта теорема, особенно в иностранной или переводной литературе, называется также теоремой Ампера или законом Ампера о циркуляции (англ. Ampère’s circuital law). Последнее название подразумевает рассмотрение закона Ампера в качестве более фундаментального утверждения, чем закон Био — Савара — Лапласа, который в свою очередь рассматривается уже в качестве следствия (что, в целом, соответствует современному варианту построения электродинамики).
Для общего случая (классической) электродинамики формула должна быть дополнена в правой части членом, содержащим производную по времени от электрического поля (см. уравнения Максвелла, а также параграф «Обобщение» ниже). В таком дополненном виде она представляет собой четвёртое уравнение Максвелла в интегральной форме.