2.4. Основные положения волновой теории

передачи света по световодам

2.4.1. Основные понятия

Строгое решение задач распространения электромагнитной энергии по оптическим кабелям требует применения классической электродинамики и уравнений Максвелла. На основе электродинамики можно рассмотреть практически все вопросы передачи, излучения, влияния и поглощения в ОК. Правда, во многих случаях очень сложно искать точные решения на базе электродинамики. Для практики в свое время были разработаны приближенные методы решения задач различных классов. Таким наиболее характерным методом является метод теории геометрической оптики, когда (квазиоптический режим) совершается переход от волновых электродинамических процессов к лучевым процессам (λ→0). При λ→0 области очень высоких частот (свыше 10¹³ Гц) справедливы уравнения геометрической оптики. Однако квазиоптический режим передачи по ОВ является предельным случаем строгих уравнений электродинамики.

Носителем электромагнитной энергии, широко используемой в современной радиоэлектронике, электросвязи и высоковольтной технике, является электромагнитное поле. Электромагнитное поле — это особый вид материи, оказывающий силовое воздействие на заряженные частицы и обладающий энергией, массой, скоростью, т.е. всеми свойствами материи. Поле отличается непрерывным распределением в пространстве (электромагнитные волны) и обнаруживает дискретность структуры (фотоны). Электромагнитное поле представляет собой единство двух составляющих — электрического и магнитного полей. Электрическое поле (Е) характеризуется силовым взаимодейс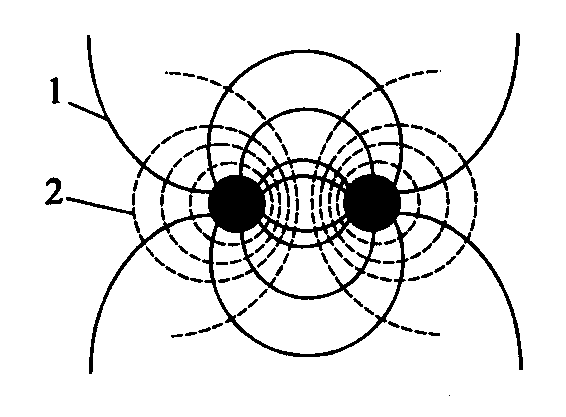 твием как с неподвижными, так и с движущимися зарядами. Магнитное поле (Н) характеризуется силовым взаимодействием лишь с движущимися зарядами. Электрические и магнитные поля связаны с определенными количествами электромагнитной энергии. В различных случаях может преобладать тот или иной вид энергии (электрической или магнитной).

Р

Рис. 2.17. Линии полей:

1-потенциальные;

2-вихревые

азличают два основных типа полей: потенциальное и вихревое. Потенциальное поле тесно связано со своим источником. Линии поля имеют начало и конец. Линии вихревого поля замыкаются по соленоиду, всегда непрерывны и не имеют начала и конца (рис. 2.17). Электростатическое поле является чисто потенциальным, а магнитное — чисто вихревым. Переменное электромагнитное поле в общем случае является суперпозицией потенциального поля электрических зарядов и вихревого поля индукции.

Электрические и магнитные свойства среды характеризуются тремя параметрами: диэлектрической проницаемостью (ε), магнитной проницаемостью (μ) и электрической проводимостью (σ).

Оптическая мощность сигнала, передаваемая по ОВ, описывается векторами напряженности (E ) и индукции (D ) электрического поля, а также векторами напряженности (Н) и индукции (В) магнитного поля. Последние связаны между собой и параметрами среды распространения следующими уравнениями Максвелла, при условии, что проводимость среды σ = 0:

(2.16)

(2.17)

(2.18)

(2.19)

(2.20)

(2.21)

Диэлектрическая и магнитная проницаемости описывают материалы, используемые в ВОСП, которые могут быть линейными и нелинейными, изотропными и анизотропными, однородными и неоднородными, дисперсионными и недисперсионными. У абсолютного большинства материалов, используемых в ВОСП, μ=μ₀ - магнитная проницаемость вакуума.

В зависимости от свойств параметров ε, μ и σ различают следующие среды:

• линейные, в которых параметры ε, μ и σ не зависят от величины электрического и магнитного полей;

• нелинейные, в которых параметры ε, μ и σ (или хотя бы один из них) зависят от величины электрического или магнитного полей.

Все реальные среды, по существу, являются нелинейными. Однако при не очень сильных полях во многих случаях можно пренебречь зависимостью с, и и ч от величины электрического и магнитного полей и считать, что рассматриваемая среда линейна.(В дальнейшем будут рассматриваться только линейные среды.) Линейные среды делятся на однородные и неоднородные, изотропные и анизотропные.

Однородными называют среды, параметры ε, μ и σ которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках. Среды, у которых хотя бы один из параметров ε, μ или σ является функцией координат, называют неоднородными. Несмотря на то, что кварц является однородной средой, оптическое волокно неоднородно из-за того, что показатели преломления сердцевины и оболочки различны. Поэтому области сердцевины и оболочки в волокне со ступенчато изменяющимся показателем преломления могут рассматриваться раздельно как однородные среды, в то время как в градиентном волокне это допущение неприемлемо, ввиду его неоднородной сердцевины.

Если свойства среды одинаковы по разным направлениям, то среду называют изотропной. Соответственно среды, свойства которых различны по разным направлениям, называют анизотропными. В изотропных средах вектор электрической поляризации ( р) и вектор (E), векторы (D) и (Е), а также векторы магнитной поляризации (М) и (Н), векторы (В ) и (Н ) параллельны, в анизотропных средах они могут быть непараллельными. В изотропных средах параметры ε, μ и σ — скалярные величины. В анизотропных средах, по крайней мере, один из этих параметров является тензором.

В кристаллическом диэлектрике тензором является диэлектрическая проницаемость ε. В общем случае ее записывают в виде матрицы:

(2.22)

При этом форма уравнения (2.18) остается прежней:

(2.23)

Для того чтобы записать уравнение (2.23) в проекциях на оси прямоугольной системы координат х, у, z, нужно раскрыть правую часть уравнения (2.23) по обычным правилам умножения матрицы. В результате получим

(2.24)

Непараллельность векторов D и Е (а также р и Е) в анизотропной среде объясняется тем, что в общем случае направление возникающего в результате поляризации анизотропной среды вторичного электрического поля, созданного связанными зарядами вещества, составляет некоторый угол (отличной от 0 и π) с направлением первичного электрического поля.

Таким образом, в изотропной среде электромагнитные свойства, такие как показатель преломления, одинаковы во всех направлениях, а Е и р являются векторами одинаковой ориентации, и так как кварц представляет собой изотропную среду, идеально цилиндрическое оптическое волокно также является изотропным.

Среда, показатели преломления которой вдоль двух разных направлений соответствующей системы координат, например вдоль осей х и у, различны, называется двулучепреломляющей, поэтому оптическое волокно, не обладающее цилиндрической системой, также является двулучепреломляющим. Двулучепреломление ряда материалов, например ниобата лития, используется в таких волоконно-оптических компонентах, как модуляторы, изоляторы и настраиваемые фильтры.

Среда, в которой ε=const, т.е. однородная по координатам пространства и не зависящая от частоты, называется однородной недисперсионной средой. В ней все частотные составляющие сигнала распространяются с одной и той же фазовой скоростью. Следовательно, сигнал не претерпевает дисперсии. Большинство оптических сред характеризуется тем, что ε = ε (ω) и ν= ν(ω) являются функциями от частоты. Это значит, что косинусоидальные волны

(2.25)

разных частот распространяются с различными фазовыми скоростями, что приводит к расширению сигнала, т.е. к появлению дисперсии.

В выражении (2.25): А — амплитуда волны; ω — круговая частота; n — единичный вектор, нормальный к плоскости, в которой находится плоская волна; r — координата точки наблюдения.