Векторний добуток

Означення 17. Векторним добутком векторів і ˟ або ) називається вектор , який задовольняє умовам:

а) вектор перпендикулярний кожному з векторів і а тим самим перпендикулярний площині паралелограма, побудованого на векторах і (рис. 3.1.17, а); b) модуль вектора в числовому вираженні дорівнює площі паралелограма, побудованого на векторах і · , де 𝜑 – кут між векторами (рис. 3.1.17, б); c) вектор направлений таким чином, що з кінця вектора найкоротший поворот від вектора до вектора видно проти годинникової стрілки (вектори ).

Із означення векторного добутку випливає, що якщо кут 𝜑=0, то = · =0⇨ = , а при

= · = ·

Звідси одержимо наступне твердження.

Твердження 9. Вектори і колінеарні тоді і тільки тоді, коли їх векторний добуток дорівнює нулю: || ⇔ .

Безпосередньо з твердження маємо важливе співвідношення:

Враховуючи твердження 9 і те, що координатні орти взаємно перпендикулярні і мають одиничну довжину, для векторних добутків цих векторів матимемо наступні співвідношення:

,

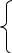
Рис. 3.1.17

Властивості векторного добутку

1. З означення векторного добутку (пункт с) випливає, що вектори і мають протилежні напрями, тобто = - . Отже для векторного добутку не виконується переставна властивість.

2. - розподільна властивість.

3. λ( ) – сполучна властивість.

Нехай вектори і задані в координатній формі: , . Тоді векторний добуток векторів і визначається за формулою:

= - =( +( .

(3.1.14)

Умова колінеарності у координатній формі матиме вигляд:

⇔ = =

(3.1.15)

Векторний добуток має також простий геометричний і фізичний зміст..

З означення векторного добутку (пункт b) можна одержати формули площ паралелограма і трикутника:

=

(3.1.16)

Якщо в точці А прикладена сила О – деяка точка простору, то момент сили відносно цієї точки О дорівнює:

Мішаний добуток векторів

Означення 18. Мішаним добутком трьох векторів , , і - називається число, одержане векторним множенням перших двох векторів з наступним множенням на третій вектор скалярно: =( )·

Властивості мішаного добутку векторів

Твердження 10. Абсолютна величина мішаного добутку дорівнює об’єму паралелепіпеда, побудованого на векторах , , і що є його сторонами (рис. 3.1.17, в):

(3.1.17)

Дійсно, для мішаного добутку маємо наступні співвідношення:

( )· = · , де . Але · · +

Де знак “+”, чи “-” береться в залежності від того, яку трійку складають вектори , , - праву чи ліву. Крім того, = , що і доводить твердження 10.

Наслідок. Об’єм тетраедра, побудованого на векторах , , і обчислюється за формулою: V=

1. ( )· =( )· =( )·

   При циклічній перестановці співмножників мішаний добуток векторів не змінюється:

Дійсно, при цьому не змінюються параметри паралелепіпеда і орієнтація векторів, що означає незмінність об’єму паралелепіпеда.

2. У мішаному добутку векторів знаки векторного і скалярного добутків можна міняти місцями:

( )· = ·( )

Це випливає з рівності об’ємів паралелепіпедів і однакової орієнтації відповідних трійок векторів: ( )·

Якщо вектори задані координатами , , , то мішаний добуток обчислюється за формулою:

=

(3.1.18)

Дійсно за означенням мішаного добутку маємо:

( )· = ·( )= - + =

Твердження 11. Вектори , , і компланарні тоді і тільки тоді, коли їх мішаний добуток дорівнює нулю: , , компланарні⇔

Це твердження має простий геометричний зміст: якщо вектори компланарні, то вони розміщені на одній площині і об’єм паралелепіпеда, побудованого на цих векторах дорівнюватиме нулю.

Твердження 12. Якщо , то вектори , , утворюють праву трійку не компланарних векторів, якщо ж - ліву.

Таким чином, поняття векторного та мішаного добутків можна використовувати для обчислення площ і об’ємів різних геометричних фігур.