7.2.2.2 Возникновение отрицательного сопротивления в лпд.

Пусть к ЛПД приложено постоянное напряжение , приводящее к ударной ионизации в переходе. Нас интересует, будет ли сопротивление прибора по переменной составляющей отрицательным, т.е. будет ли <0 , где - амплитуда небольшого переменного напряжения на приборе ( ); - амплитуда 1-й гармоники тока, проходящего через ЛПД ( ), т.е. ток в общем случае может отставать по фазе на угол от напряжения и поэтому при записи мы используем комплексное представление амплитуды тока . На рис.7.15 изображена упрощенная модель ЛПД: I) - область умножения, где происходит лавинное умножение тока; 2) - область дрейфа, в которой отсутствует генерация носителей, а имеющиеся носители тока движутся со скоростями насыщения; 3) - пассивная область, отражающая нежелательное паразитное пассивное сопротивление области .

Рис. 7.15

Сопротивление где - сопротивление слоя умножения; - сопротивление области дрейфа; -активное сопротивление потерь пассивной области. Рассмотрим сопротивления этих областей:

, где - амплитуда переменного напряжения на слое умножения; - амплитуда переменного тока, проходящего через слой умножения. Ток в любом сечении слоя умножения есть сумма конвекционной составляющей тока, вызванной движением электронов и дырок, и тока смещения (7.5). Поскольку слой умножения достаточно узок, то можно считать , что не зависит от координаты и , где - ширина слоя умножения. Поэтому в первом приближении можно считать, что как ток смещения так и конвекционный ток не зависят от . На рис. 7.16 изображена эквивалентная схема слоя умножения. Ток смещения проходит через емкость , а конвекционный ток через индуктивность . Это означает, что ток отстает на 90 градусов от напряжения .

Рис. 7.16

Такое отставание вызвано следующими причинами. Переменное напряжение создает переменное электрическое поле . Поскольку коэффициенты ударной ионизации зависят от электрического поля (см. рис. 7.10), то появляется переменная составляющая коэффициентов ударной ионизации и . В соответствии с уравнением непрерывности (7.7) это должно приводить к переменной составляющей концентрации и . В соответствии с (7.7) и должны отставать по фазе на 90 градусов от и . Поскольку переменная составляющая дрейфового тока в соответствии с (7.5) равна:

,

где - скорость насыщения носителей, то это приводит к отставанию тока от напряжения . Аналогичные выводы вытекают из решения основного уравнения лавинного тока приведенного в приложении П1. В соответствии с приведенными там выкладками , где - постоянная составляющая конвекционного тока.

, где . Ток смещения = вызван переменной составляющей напряжения . Конвекционный ток = не зависит от переменной составляющей напряжения , поскольку - скорость насыщения, практически независящая от электрического поля, - переменная составляющая концентрации, определяется «сгустками» лавинного тока умножения дрейфующих со скоростью к коллектору. Поэтому соотношение между и может быть таким, что <0. На рис. 7.17 изображены векторные диаграммы поясняющие условия возникновения отрицательного сопротивления в дрейфовой области.

Рис. 7.17.

Если частота переменного напряжения меньше лавинной частоты , то сопротивление лавинной области будет иметь индуктивный характер. Сопротивление дрейфовой области перед началом лавинного пробоя будет иметь емкостный характер. Поэтому будет противоположно по фазе . Лавинный ток отстает на 90 градусов от . Ток отстает от на угол , где - расстояние от границы раздела области умножения и дрейфовой области. Как видно из рис. 7.17 а), в этом случае >0. Если частота переменного напряжения больше лавинной частоты , то фазовые соотношения обеспечивают условия для <0, как видно из рис. 7.17б). Физически это означает, что "сгусток" электронов выходит из .слоя умножения и при движении к слою большую часть времени находится в тормозящем переменном электрическом поле, совпадающем по направлений со скоростью движения "сгустка" . В этом случае электроны передают часть своей энергии переменному электрическому полю. Поскольку скорость электронов поддерживается равной за счет источника постоянного напряжения и, то происходит перекачка энергии от источника постоянного смещения в энергию колебаний, в чем, вообще и заключается физический смысл отрицательного сопротивления.

Используя уравнения полного тока (7.5) несложно получить явное выражение для .

Пусть . Ток в любом сечении может быть представлен суммой конвекционного тока и тока смещения:

, (7.10)

где , - комплексная амплитуда переменной составляющей конвекционного тока, равная комплексной амплитуде переменной составляющей лавинного тока , - комплексная амплитуда переменной составляющей напряженности электрического поля. Если ввести коэффициент , то из (7.10) нетрудно получить:

. (7.11)

Учитывая, что и , из (7.11) получаем :

, (7.12)

где = - угол пролета дрейфового пространства, = - емкость области дрейфа.

На рис. 7.18 представлены зависимости активной и реактивной составляющих от частоты.

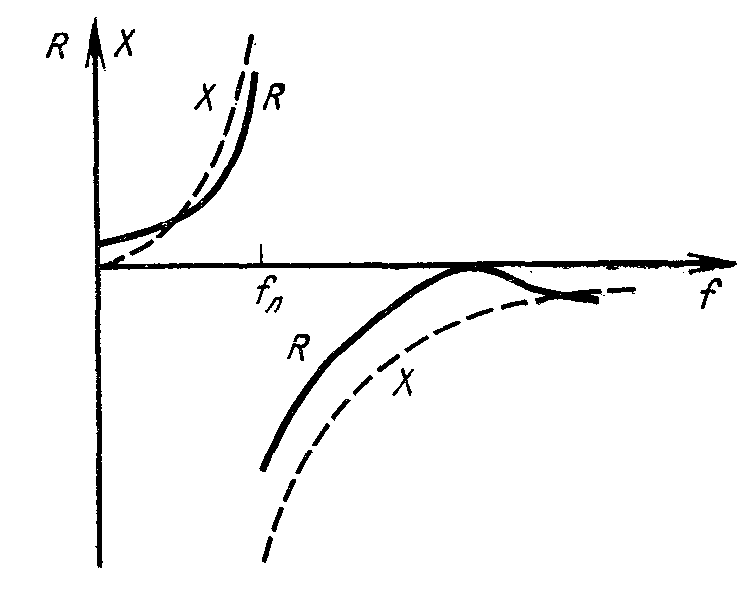
Рис. 7.18

Видно что при > = <0.

На рис. 7.19 представлена зависимость от при > .

Рис. 7.19

Видно, что максимальное отрицательное сопротивление достигается при . Поэтому для построения генератора на ЛПД необходимо выбирать длину дрейфовой области из условия .