Условная вероятность.

Начнем с примера. Пусть эксперимент состоит в троекратном подбрасывании монеты. Вероятность того, что герб выпадет 1 раз – событие А= (грр, ргр, ррг) равна 3/8. Предположим, что об исходе эксперимента дополнительно известно, что произошло событие В – «число выпавших гербов нечетно», В=(грр, ргр, ррг, ггг). Какова вероятность события А при наличии этой дополнительной информации? В рамках классической схемы естественно принять новую вероятность события А равной 3/4. Событие В при этом рассматриваем как новое пространство элементарных исходов.

Вероятность события А при условии, что произошло событие В, имеет вид

.

Рассмотрим более общий пример. Пусть задана классическая схема с n исходами. Событие А состоит из r исходов, событие В – из m исходов, а событие АВ – из k исходов. Вероятность события А при условии, что произошло событие В, естественно определить в виде

.

Определение: Пусть задано ВП и пусть А и В – произвольные события.

Если Р(В)>0, то условная вероятность события А, при условии, что произошло событие В, по определению полагается равной

.

Определение условной вероятности является согласованным с определением независимости событий. Для независимых событий А и В Р(А/В)=Р(А).

Формула полной вероятности. Формулы Байеса.

Формула полной вероятности позволяет получить формулу для безусловной вероятности события А когда известен ряд его условных вероятностей.

Определение: События будем называть полной системой событий, если

1.

2.

3.

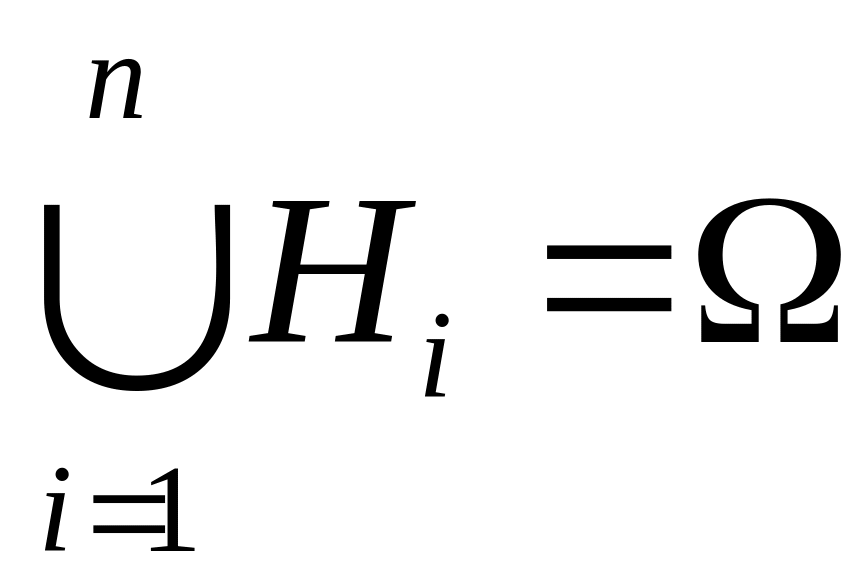
Пусть известны безусловные вероятности и условные вероятности события А, тогда

Последнее выражение называется формулой полной вероятности.

Теперь выразим через и .

Вероятности принято называть априорными, а вероятности - апостериорными.

Последнее выражение называется формулой Байеса.

Пример 3. Задача о наилучшем выборе

Предположим, что имеется m предметов, сравнивая которые наблюдатель может сказать, который предмет лучше или хуже. Наблюдатель последовательно осматривает предметы, причем, осмотрев и отвергнув некоторый предмет, нельзя к нему возвращаться. Дополнительно существует еще одно правило: нельзя останавливать свой выбор на предмете, который хуже какого-нибудь осмотренного предмета. Предположим, что, следуя описанной процедуре, наблюдатель сделал выбор, остановившись на k-ом предмете, т.е. последний из осмотренных k-ый предмет является наилучшим среди всех осмотренных. Какова вероятность, что этот выбранный предмет является наилучшим среди всех m предметов?

Решение.

Обозначим В событие, состоящее в том, что k-ый предмет является наилучшим среди всех осмотренных. Наблюдателю известно, что событие В произошло. Обозначим А событие, состоящее в том, что k-ый предмет является наилучшим среди всех m предметов.

Надо найти Р(А/В)= Р(АВ)/ Р(В).

Всевозможные расположения предметов при осмотре будем считать равновероятными. Считая, что номер предмета в исходной совокупности определяет его качество, исходами эксперимента можно считать различные перестановки из m чисел.

Событие А содержится в В, поэтому Р(АВ)=Р(А) и Р(А/В)= Р(А)/ Р(В).

;

Пример 4: Задача о разорении игрока.

Рассмотрим игру следующего вида. Пусть некоторое случайное испытание имеет два исхода 0 и 1 с вероятностями p и q=1-p. Игрок выбирает исход (0 или 1), после чего производится испытание. Если результатом испытания является исход, выбранный игроком, то он выигрывает 1 у.е., в противном случае он проигрывает 1 у.е. Предположим, что начальный капитал игрока составляет n у.е. и игрок ставит себе целью довести его до а у.е. Игра продолжается до тех пор, пока либо игрок наберет заранее определенную сумму в а у.е., либо разорится проиграв n у.е.

Какова вероятность того, что в конце концов игрок разорится, так и не набрав желаемую сумму в а у.е.?

Обозначим искомую вероятность через p(n). Ясно, что p(n) зависит от начального капитала n и конечной суммы а.

На первом шаге игрок может либо выиграть, либо проиграть. Используя формулу полной вероятности, получим

,

причем p(0)=1, p(a)=0.

Последнее уравнение является линейным разностным уравнением.

Для его решения необходимо решить характеристическое уравнение

.

Если корни характеристического уравнения ₁, ₂ различны, то решение разностного уравнения имеет вид

Если корни характеристического уравнения одинаковы ₁= ₂ то решение разностного уравнения имеет вид

Если корни характеристического уравнения являются комплексно сопряженными , то решение разностного уравнения имеет вид

Решая характеристическое уравнение , получим

и .

Используя граничные условия p(0)=1, p(a)=0, получим

.

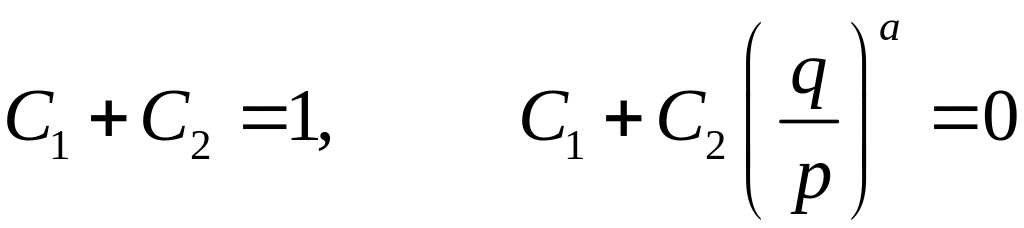Поэтому .

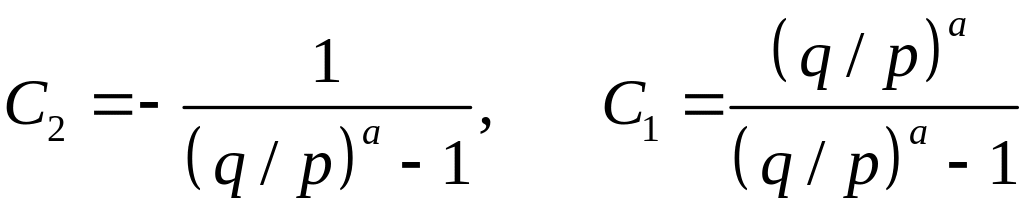Т.О. вероятность разорения имеет вид:

.

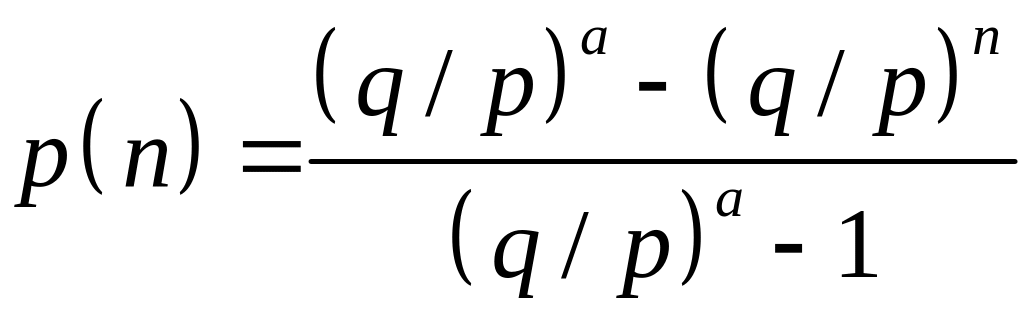Полученное решение справедливо при .

При p=q=1/2 корни характеристического уравнения одинаковы ₁= ₂1 и решение разностного уравнения имеет вид

Используя граничные условия , получим

.

18