План лекции

1. Алгебра и -алгебра событий

2. Аксиоматическое определение вероятности. Свойства вероятности.

3. Условная вероятность. Независимость событий.

4. Формулы полной вероятности. Формула Байеса.

Наша цель – определить вероятность таким образом, чтобы рассмотренные ранее подходы были бы частным случаем этого определения. Для этого придется ввести некоторые ограничения на то, какие подмножества множества пространства элементарных исходов мы будем считать событиями.

Пусть пространство элементарных исходов есть некоторое множество , а F – некоторая система подмножеств данного множества.

F называется алгеброй, если

А1.

А2. Из того, что и следует что .

А3. Если , то .

В условии А2 достаточно требовать выполнение только одного из двух условий. Действительно, если , , то .

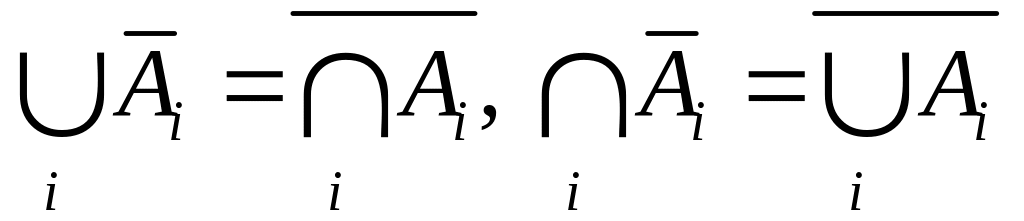( - формулы де Моргана)

F называется -алгеброй, если свойство А2 выполняется для любых последовательностей множеств;

А2’. Если есть последовательность множеств из F , то

.

Таким образом, алгебра есть класс множеств, замкнутый относительно конечного числа операций объединения, пересечения, дополнения, а -алгебра - класс множеств, замкнутый относительно счетного числа этих операций.

Если задано множество и какая-нибудь -алгебра его подмножеств, то говорят, что задано измеримое пространство .

Для того, чтобы формализовать некоторую вероятностную задачу, надо соответствующему эксперименту приписать измеримое пространство . При этом означает пространство элементарных исходов эксперимента, а -алгебра выделяет класс событий. Все подмножества , не входящие в F, событиями не являются.

Вероятность есть числовая функция, определенная на -алгебре событий и удовлетворяющая свойствам (аксиомам):

Р1.

Р2.

Р3. Если последовательность событий такова, что при , то

.

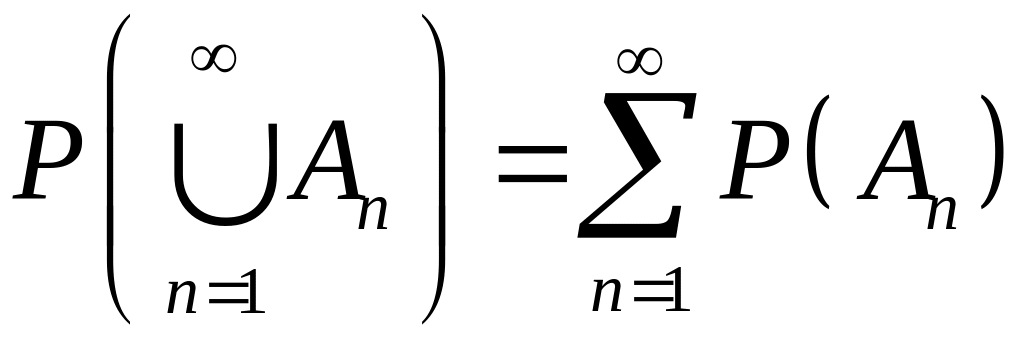Аксиома Р3 эквивалентна требованию конечной аддитивности и следующей аксиоме непрерывности.

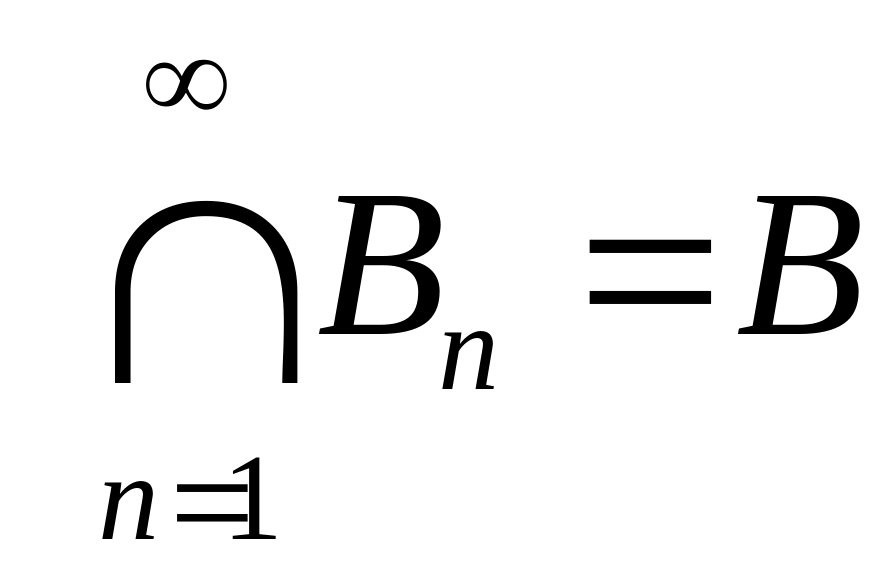Р3’. Пусть последовательность событий такова, что и , тогда при .

Доказательство эквивалентности.

1. Предположим выполненным условие счетной аддитивности Р3.

Рассмотрим убывающую последовательность событий , . Тогда последовательность событий, , k=1,2,... состоит из попарно несовместных событий и .

Согласно условию счетной аддитивности получим . Соответственно ряд - сходится. Это означает, что остаточные суммы стремятся к нулю, то есть при . Поэтому, при . Таким образом, из условия счетной аддитивности Р3 следует условие непрерывности Р3’.

2. Предположим выполненным условие непрерывности Р3’ и конечной аддитивности.

Рассмотрим последовательность несовместных событий .

Поскольку , то .

Поэтому

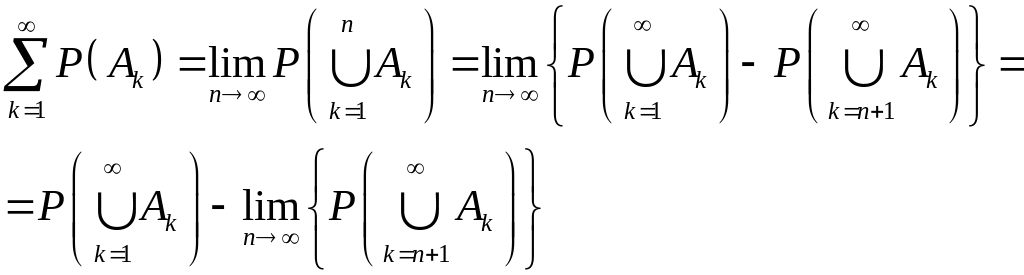Введем убывающую последовательность событий , .

Согласно Р3’ .

Поэтому

Тройка называется вероятностным пространством.

Таким образом, задание вероятностного пространства есть задание счетно-аддитивной меры на измеримом пространстве, такой, что мера равна 1.