10. Смешанные стратегии. Геометрическая интерпретация множества смешанных стратегий.

Стратегия игрока, состоящая в случайном выборе одной из его чистых стратегий, называется смешанной стратегией. Таким образом, смешанная стратегия игрока представляет собой дискретную случайную величину, значениями которой являются номера его чистых стратегий.

О

,

бозначим через Р и Q смешанные стратегии игроков А и В соответственно. Таким образом, смешанная стратегия Р задается законом распределения

1	…	i	…	m
p1	…	pi	…	pm

где p_i ≥ 0 - вероятность применения игроком А чистой стратегии A_i, и p₁ +...+ p_i +...+ р_т = 1, как сумма вероятностей несовместных событий (состоящих в выборе одной из чистых стратегий) полной группы, а смешанная стратегия Q характеризуется законом распределения

1	…	j	…	n ,
q1	…	qj	…	qn

где q_j ≥ 0 - вероятность выбора игроком В чистой стратегии B_j, q₁ +...+ q_j +...+ q_n = 1.

При условии, что множество ={А₁, ..., А_т} чистых стратегий игрока А известно, каждая его смешанная стратегия Р определяется вероятностями p₁, ..., р_т, с которыми выбираются игроком А соответствующие чистые стратегии. Поэтому смешанную стратегию Р можно отождествить с m-мерным вектором (p₁, ..., р_т), т. е. То же относится и к смешанным стратегиям игрока В:

При т = 1 игрок А обладает одной чистой стратегией A₁ и потому смешанная стратегия совпадает с чистой. Таким образом, множество смешанных стратегий состоит из единственного элемента A₁: S_A = = {A₁} - и представляет собой 0-мерный симплекс, состоящий из единственной точки - вершины А₁.

При т = 2 игрок А имеет две чистые стратегии: = {A₁, A₂}, а множество S_A смешанных стратегий есть 1-мерный симплекс с двумя вершинами А₁ и А₂, представляющий собой отрезок с концами А₁ и А₂

При т = 3 у игрока А три чистые стратегии: = {A₁, A₂, A₃}; множество S_A смешанных стратегий является 2-мерным симплексом с вершинами A₁, A₂, A₃, представляющим собой плоский правильный треугольник А₁А₂А₃ (см. рис. 3).

При т = 4 множество смешанных стратегий S_A есть 3-мерный симплекс с четырьмя вершинами A₁, A₂, A₃, А₄, представляющий собой правильный тетраэдр (см. рис. 4).

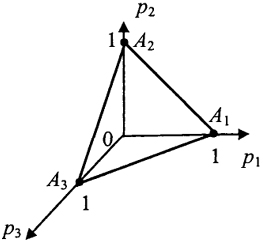
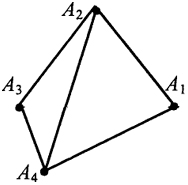
Рис. 3 Рис. 4

Аналогичная геометрическая интерпретация имеет место и для игрока В, множество чистых стратегий которого ={В₁, ..., В_п} представляет собой множество п вершин В₁, ..., В_п (n - 1)-мерного симплекса смешанных стратегий.

11. Определение выигрыш-функции в смешанных стратегиях; координатные и векторно-матричные формулы ее представления.

Ф-ия выигрыша иг-ка в смеш.стр-ях определяется как ф-ияН, заданная на декартовом произведении мн-твсмеш.стр-ийиг-ов А и В, которая ставит в соответствие каждой ситуации в смеш.стр-ях средний выигрыш иг-ка , определяемый выражением:

(как математическое ожидание указанной случайной величины).Т.о., ),где Если т.е. , то из (*) следует, что: Данное рав-во означает, что ф-ия выигрыша в смеш.стр-яхН совпадает на декартовом произведении с функцией выигрыша в чистых стр-яхF и, следовательно, является ее расширением (продолжением) с декартова произведения на декартово произведение .В силу этого совокупность мн-твсмеш.стр-ий иг-овА и В и ф-ий выигрыша иг-каА в смеш.стр-яхН называется смешанным расширением игры в чистых стр-ях.Функцию Н можно задать и в матричной форме: , где ) — вектор-строкаразмера , мат-ца игры размера (мат-ца выигрышей иг-каА в чистых стр-ях), вектор-столбец размера