46. Математическая модель игры с природой. Показатель благоприятности состояния природы. Матрица рисков.

Игра с природой — математическая модель ситуаций, когда осознанно действует только один игрок (обозначим его через А), принимающий решение, и когда исход игры зависит не только от решений игрока А, но и от состояния “природы” (обозначим через П), т. е. не от сознательно противодействующего противника, а от объективной, невраждебной действительности. 

Природа – это:

1. объективная действительность;

2. игрок, но не противник игрока А, потому что не действует осознанно против игрока А, а принимает неопределенным образом то или иное свое состояние, не преследуя конкретной цели и безразлично к результату игры.

Статистик – игрок в игре с природой, действующий осознанно, т.е. лицо, принимающее решение (игрок А).

Одним из важных предположений в теории игр с природой является предположение о том, что в любой момент времени природа П может находиться только в одном (но неизвестно, в каком) из n состояний П1, П2, …, П_n, то есть состояния природы разделены между собой во времени. Совокупность состояний природы П формируется либо на основе имеющегося опыта анализа состояний природы, либо в результате предположений и интуиции экспертов.

Для описания игры с природой необходимо также множество стратегий игрока A: .

Результаты реализации стратегий при различных состояниях природы могут быть описаны матрицей V:

.

Будем предполагать, что в платёжной матрице игры представлены выигрыши лица, принимающего решения.

Показателем благоприятности состояния природы для увеличения выигрыша называется наибольший выигрыш при этом состоянии, т.е. наибольший элемент в j-м столбце матрицы игры: , ,

Риском игрока A при выборе им стратегии в условиях состояния природы называется разность между показателем благоприятности состояния природы и выигрышем , т.е. разность между выигрышем, который игрок A получил бы, если бы знал заранее, что природа примет состояние , и выигрышем, который он получит при этом же состоянии , выбрав стратегию , т.е. .

Матрица рисков

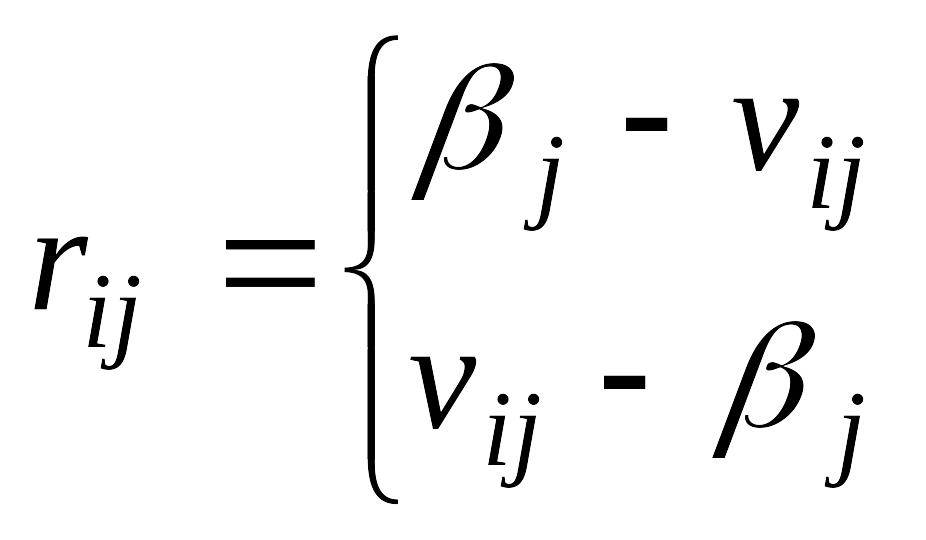
47. Критерий Байеса оптимальности чистых стратегиях относительно выигрышей.

Пусть известны состояния П­₁ … П­_n и вероятности q₁ … q_{n ,} с которыми природа П реализует эти состояния. Тогда мы находимся в ситуации принятия решения в условиях риска. Показателем эффективности стратегии по критерию Байеса относительно выигрышей называется среднее значение, или математическое ожидание выигрыша i-й строки с учётом вероятностей всех возможных состояний природы: , .

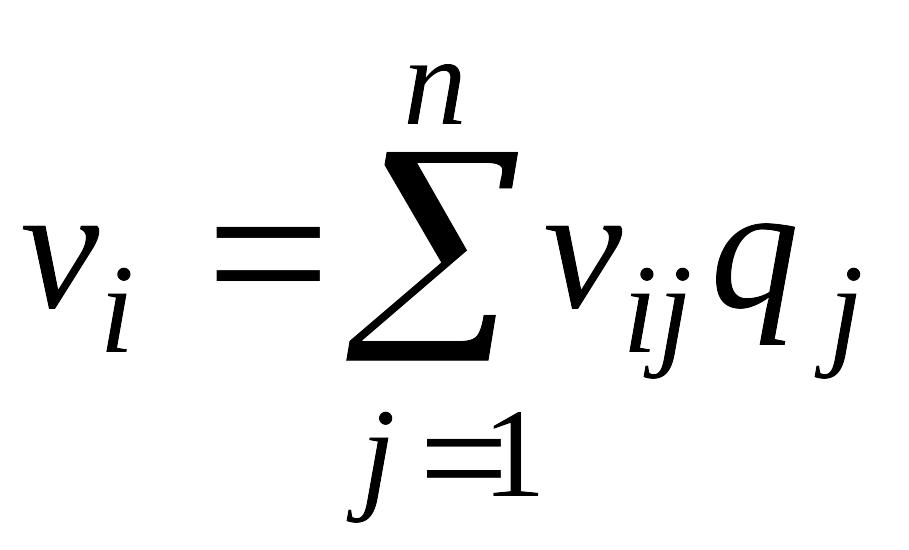Оптимальной среди чистых стратегий по критерию Байеса относительно выигрышей считается стратегия с максимальным показателем эффективности: 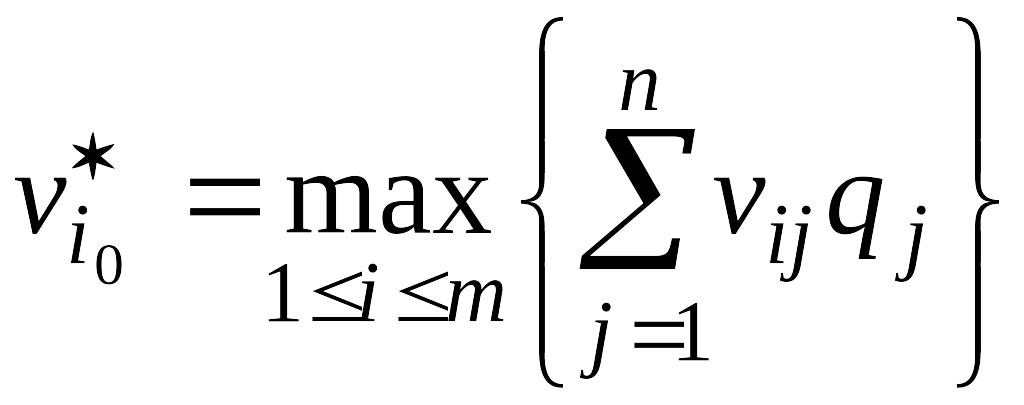(матрица выигрышей), 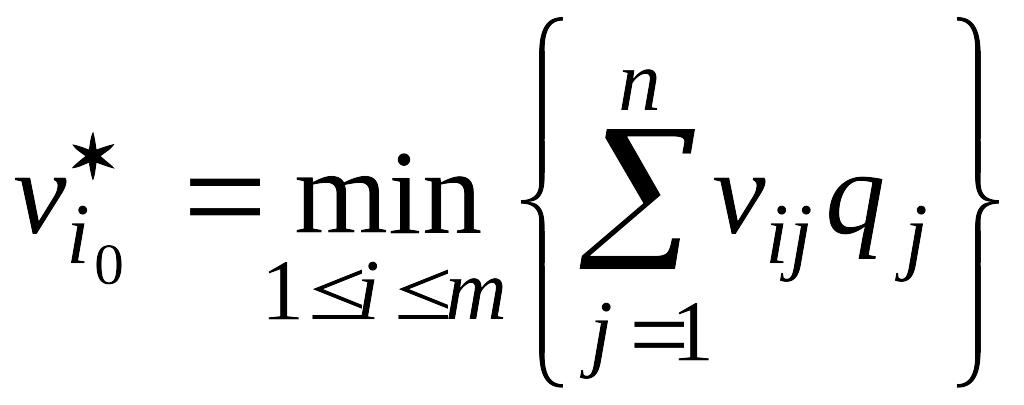(матрица потерь).

Критерий Байеса относительно выигрышей и относительно рисков эквивалентны, т.е. если стратегия S_io является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.

Пример.

	,	,	,	vi
S1	2	6	4	4,6
S2	5	1	3	2,4

Для матрицы выигрышей: , . Для матрицы потерь:

,