38. Теорема об аналитическом методе нахождения цены игры 2 и оптимальных стратегий игрока а.

Если через макс. точку N нижней огибающей отрезков а_1jа_2j, j=1,..., п, порождаемых чистыми стр.миB_j, j=1,..., п, иг-каВ, проходят два каких-либо отрезка и , j₁≠j₂, j₁, j₂ {1, …, n}, то абсцисса точки N (1. 2)и, следовательно, (1. 2) а цена игры (1. 2)

39. Доказательство теоремы об аналитическом методе нахождения цены игры 2 и оптимальных стратегий игрока в и её следствия.

Пусть через макс. точку N нижней огибающейа_1jа_2j, j=1,..., п, порождаемых чистыми стр.миB_j,j=1,..., п, иг-каВ, проходят два каких-либо отрезка и , j₁≠j₂, j₁, j₂ {1, …, n}. Для того чтобы смеш. стр. иг-ка B, где (1.10), (1.11), (1.12) была опт.⇔чтобы отрезки и имели разные наклоны.

Док-во. Цена игры Т.к. цена игры Vпредставляет собой ординату точки M, то для вычисления Vдостаточно в правую часть одного из рав-тв или подставить . Подставляя в правую часть рав-ва , получим Необходимость. Пусть смеш. стр. иг-ка В, в которой вероятности , j=1,..., n, определяются ф-лами (1.10), (1.11) и (1.12), является опт..

Нам надо доказать, что отрезки и имеютразные наклоны. Предположим противное: эти отрезки имеют одинаковые наклоны.

Так как уравнениями отрезков и являются соответственно уравнения (1.8) и (1.9), то угловые коэффициенты этих отрезков соответственно равны (1.13), (1.14)

Т.к. (по предположению) отрезки и имеют одинаковые наклоны, то и либо оба положительны, либо оба отрицательны, либо оба равны нулю.

+следствие

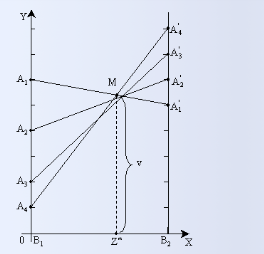
40. Геометрический метод нахождения цены игры m2 и оптимальных стратегий игрока в.

1. Берем горизонтальный отрезок [0,1].

2. Через концы отрезка [0,1] проводим к нему два перпендикуляра: левый и правый.

3. На левом перпендикуляре, лежащем на вертикальной числовой оси, от точки 0 его пересечения с отрезком [0,1] откладываем все элементы первой строки мат-цыА.

4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второй строки мат-цыА.

5. Каждую пару точек, изображающих элементы а_i1 и а_i2, стоящие в i-й строке мат-цыА, соединяем отрезком а_i1а_i2. Т.о., будут построены m отрезков, представляющих собой графики m линейных функций 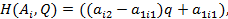q [0,1], i=1,..., m. (2. 2)

6. Если все отрезки а_i1а_i2, i=1,..., m, — неубывающие (имеют неотрицательный наклон), то стр.B₁доминирует стр-июB₂.Если все отрезки а_i1а_i2, i=1,..., m, — возрастающие (имеют положительный наклон), то стр.B₁строго до минирует стр-июB₂.

7. Если все отрезки а_i1а_i2, i=1,..., m, — невозрастающие (имеют неположительный наклон), то стр.B₂ до минирует стр-июB₁.Если все отрезки а_i1а_i2, i=1,..., m, — убывающие (имеют отрицательный наклон), то стр.B₁ строго до минирует стр-июB₂.

8. Если отрезок 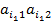лежит не ниже отрезка 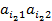, i₁≠i₂, i₁, i₂ {1, …, m},то стр.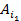 доминирует стр-ию 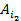.Если отрезок лежит выше отрезка , i₁≠i₂, i₁, i₂ {1, …, m}, то стр. строго доминирует стр-ию .Находим (выделяем) верхнюю огибающую (2.1) семейства отрезков (2.4), которая в общем случае будет представлять собой выпуклую вниз ломаную, а, в частности, может быть и отрезком.

9. Наверхней огибающей находим минимальную (низшую) точку (или точки).

10. Абсцисса q⁰ этой точки (удовлетворяющая рав-тву (2.2)) является вероятностью выбора игроком B чистой стр-ииB₂ в опт.смеш.стр-ииQ⁰=(1-q⁰, q⁰).

11. Ордината низшей точки верхней огибающей является ценой игры V(см.(2.3)).

12. Верхний из нижних концов отрезков а_i1а_i2, 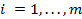есть нижняя цена игры в чистых стр-ях α.

13. Нижний из концов верхней огибающей (лежащих на перпендикулярах), есть верхняя цена игры в чистых стр-ях β.

14. Элемент мат-цыА, представленный на рисунке точкой являющейся нижним концом отрезка, на котором она лежит, и верхним на перпендикуляре, которому она принадлежит, является седл. точкой игры. В этом случае чистаястр.иг-каА, номер которой совпадает с первым индексом седл. точки, является опт..