33. Доказательство признака существования седловой точки в игре 22 в терминах сумм элементов главной и побочной диагоналей матрицы игры и его следствие.

Т. Для того чтобы у мат-цы размером 22 ∃а седл. точка, достаточно, чтобы сумма элементов главной диагонали мат-цы равнялась сумме элементов ее побочной диагонали: (1).

Док-во. Из рав-ва(1) получим (2). Возможны случаи: (3) или (4).

В случае (3) и (2) получим нерав-во , которое вместе с нерав-вом (3) означает, что второй столбец мат-цы доминируется ее первым столбцом. Тогда на основании следствия Т о доминируемых стр-ях существует опт.смеш.стр.иг-ка , в которую чистая стр. входит с нулевой вероятностью. Следовательно, стр. пассивна, и потому в силуТ о сущ-ииседл. точки в терминах пассивных стр-ях у мат-цы существует седл. точка. В случае (4), из (2) вытекает нерав-во , которое вместе с (4) означает строгую доминируемость первого столбца мат-цы ее вторым столбцом. А потому на основании того же следствия стр. является пассивной и, следовательно, по указанной вышеТ, у мат-цы существует седл. точка.

34. Доказательство теоремы об аналитическом решении игры 22 без седловой точки в смешанных стратегиях и ее следствия для симметрической и двоякосимметрической матрицы игры.

Т: Пусть мат-ца А размером 2x2 не имеет седл. точки. Тогда каждый из иг-ов А и В обладает единственной опт.смеш. стратегией соответственно , где , (1), , (2), а цена игры в смеш.стр-яхV определяется формулой: (3)

Док-во. Так как мат-ца не имеет седл. точки, то нижняя цена игры в чистыхстр-ях меньше верхней цены игры в чистых стр-ях: решения игры в чистых стр-ях не существует и надо искать решение игры в смеш.стр-ях.

В этом случае выполняется условие (*).Пусть , — оптим смешанные стр-иииг-овАи В и V — цена игры. Тогда по определению опт.стр-ий . Т.к. мат-цаАне имеет седл. точек, то в силу Т о сущ-ииседл. точки в терминах пассивных стр-ий, пассивных стр-ий в игре не существует. Поэтому стр-ииВ₁и В₂активны. Тогда , j=1,2. Записывая ле­вые части этих рав-тв по формуле и присоединяя к ним условие получим систему трех ли­нейных алгебраических уравнений:

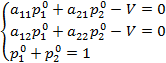Найдем решение системы по ф-лам крамера и имеет единственное решение, т.к. определитель системы ≠0 ( ). Определитель этой системы:

, , . Тогда: , , . Откуда и получаем требуемые ф-лы (1) и (3). Док-ва формул (2) аналогичные.

35. Геометрический метод нахождения цены игры 22 и оптимальных стратегий игрока а.

1.Берем горизонтальный отрезок [0,1].( )

2.В концах отрезка [0,1] проводим к нему два перпендикуляра: левый, соответствующий чист.стр-ииA₁, и правый- A₂,.

3.На левом перпендикуляре от его пересечения с отрезком [0,1] в точке 0 откладываем элементы a₁₁, a₁₂ первой строки мат-цы А.

4.На правом перпендикуляре от его пересечения с отрезком [0,1] в точке 1 откладываем элементы a₂₁, a₂₂ второй строки мат-цы А.

5.Соединяем точки, изображающие элементы с одинаковыми вторыми индексами (элементы, стоящие в одном и том же столбце мат-цы А). В результате получаем отрезки a₁₁a₁₂ и a₂₁a₂₂

Прямые на графике:

6.Если отрезкиa₁₁a₁₂ и a₂₁a₂₂неубывающие: , то стр.A₂ доминирует стр-июA₁

Если отрезкиa₁₁a₁₂ и a₂₁a₂₂возрастающие: , то стр.A₂ строго доминирует стр-июA₁

7.Если отрезокa₁₁a₂₁ лежит не ниже отрезкаa₁₂a₂₂, то стр.B₂ доминирует стр-июB₁

Если отрезокa₁₁a₂₁ лежит выше отрезкаa₁₂a_22, не пересекается с ним, то стр.B₂ строго доминирует стр-июB₁

8.Пок-льэфф-тисмеш.стр-ииР=(1-р,p)

- это ф-ия от р, являющаяся нижней огибающей ф-ии Н(Р, В₁) и Н(Р, В₂) (отрезковa₁₁a₂₁ и a₁₂a₂₂ соответственно).

9.Находим наивысшие точки нижней огибающей.

10.Проектируем их ортогонально на горизонтальный отрезок [0,1].

11.Полученные проекции определяют опт.стр-ии иг-ка А.

12.Ордината наивысшей точки огибающей равна цене игры

= _.

13.Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стр-ях .

14.Нижний из двух верхних концов отрезковa₁₁a₂₁ и a₁₂a₂₂ есть верхняя цена игры в чистых стр-ях

15.Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезкаa₁₁a₂₁ и a₁₂a₂₂, на котором он лежит, то этот элемент является седл. точкой. В этом случае чистаястр.иг-ка В, номер которой совпадает со вторым индексом седл. точки, является опт..