2. Числовые характеристики дискретных случайных величин

Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности: M(X) = x₁p₁ + x₂p₂ + ... + x_np_n

Свойства математического ожидания. 1)Математическое ожидание постоянной величины равно самой величине: М(С) = С 2) Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = С·М(Х) 3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых: М(Х₁ + Х₂ + …+ Х_n) = М(Х₁) + М(Х₂) + ... + М(Х_n) 4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей: М(Х₁ · Х₂ · ... · Х_n) = М(Х₁) · М(Х₂) · ... · М(Х_n)

Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(X) = (x₁ - M(X))²p₁ + (x₂ - M(X))²p₂ + ... + (x_n- M(X))²p_n = x²₁p₁ + x²₂p₂ + ... + x²_np_n - [M(X)]²

Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х₁ ± Х₂ ± ... ± Х_n) = D(Х₁) + D(Х₂) + ... + D(Х_n)

49. Непрерывные случайные величины.

Определение. Непрерывной случайной величиной называется случайная величина, которая может принять любое значение из заданного числового отрезка.

Вероятность любого отдельного значения непрерывной случайной величины равна нулю. Этот вывод можно получить из соотношения (1.24), согласно которому   для дискретных случайных величин.

Если неограниченно уменьшать отрезок (a, b), полагая  , то в пределе получим не вероятность попадания на участок, а вероятность того, что случайная величина X = a, т. е.

.

Если функция F(x) непрерывна в точке а, то этот предел равен нулю.

Непрерывными случайными величинами называют еще величины, функция распределения которых везде непрерывна. Таким образом, обладать нулевой вероятностью могут не только невозможные (как определялось ранее), а и возможные события. Это появляется при рассмотрении экспериментов, не сводящихся к схеме случаев.

Как указывалось ранее, закон распределения для непрерывной случайной величины может быть задан с помощью функции распределения.

Кроме этого, для задания закона распределения непрерывной случайной величины используется функция f(x) = F^/(x), которая называется плотностью вероятности и которая является производной от функции распределения. Поэтому ее еще называют дифференциальной функцией, а функцию распределения называют интегральной функцией.

Кривая, изображающая плотность распределения, называется кривой распределения; пример кривой распределения представлен на рис. 1.7.

Рис. 1.7. График плотности распределения, или кривая распределения

Вероятность попадания непрерывной случайной величины на отрезок от a до b определяется в виде

.

(1.25)

Геометрически вероятность попадания случайной величины X на участок (a, b) равна площади под кривой распределения, опирающейся на этот участок (см. рис. 1.8).

Рис. 1.8. Геометрическая интерпретация вероятности попадания случайной величины на отрезок от a до b

Заметим, что f(c) - величина плотности распределения в точке с - не определяет значение P(X=c), как в случае дискретной случайной величины. Для непрерывных случайных величин вероятность определяется для некоторого интервала и, как уже указывалось, P(X=c) = 0 для любого значения с.

Из этого следует, что не имеет значения, включаются точки a и b в интервал или нет, т. е.

.

50. Ряды Фурье.

Ряд Фурье — представление произвольной функции   с периодом   в виде ряда

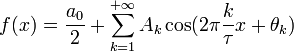
Этот ряд может быть также переписан в виде

.

где

 — амплитуда k-го гармонического колебания,

 — круговая частота гармонического колебания,

 — начальная фаза k-го колебания,

 — k-я комплексная амплитуда

В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису. Существует множество систем ортогональных функций: Уолша, Лагера, Котельникова и др.

Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.

Сходимость ряда Фурье в точке

Пусть f (x) является кусочно гладкой функцией в интервале [−π, π]. Тогда для любого 

где f (x₀ − 0) и f (x₀ + 0) представляют собой, соответственно, левосторонний и правосторонний пределы в точке x₀.