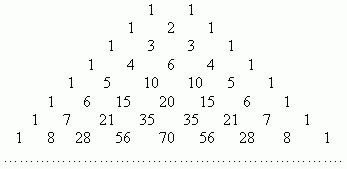Примеры задач:

Задача №1Сколькими способами можно расставить п ладей на (п х п)-доске, так, чтобы они не били друг друга!

Каждый способ задается чисел 1, 2,. . . ., п — указываются номера горизонталей занятых полей на первой, второй, . . . , n-й вертикалях.

Но число Значит, ладьи можно расставить n! способами. При п = 8 получаем 8! = 1-2-3- .4.5.6-7.8 = 40 320 способов. Ответ 40 320.

Задача№2 В слове "мама" четыре буквы. Сколько перестановок можно совершить?:

Решение: Возможные перестановки: мама, маам, ммаа, амам, аамм, амма Чтобы понять, почему Так случилось, поставим в соответствие цифрам 1 и 2 букву "м", а цифрам 3 и 4 — букву "а". Тогда, например, перестановке 1234 будет соответствовать слово ммаа, а перестановке 1324 — слово мама. Но слово ммаа соответствует не только перестановке 1234, но и еще трем перестановкам: 2134, 1243 и 2143.

Пусть цифры 1 и 2 меняются местами, то в соответствующем слове меняются местами две буквы "м", а потому само слово остается неизменным. Неизменным оно остается и при взаимной перестановке цифр 3 и 4 — при этом в слове меняются местами две буквы "а".

Всего получается 4 перестановки цифр, отвечающие одному и тому же слову.

Вот эти четверки перестановок:

1234 2134 1243 2143

1324 2314 1423 2413

1342 2341 1432 2431

3214 3124 4213 4123

3142 S241 4132 4231

3412 3421 4312 4321

Отсюда видно, что все множество из 24 перестановок цифр 1, 2, 3, 4 распадается на четверки, дающие одно и то же слово. Поэтому число различных слов равно 4!/4 = 6.

Сочетания

В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений. Число сочетаний из n элементов по k обозначаются Так, например, наборы (3-элементные сочетания, подмножества, k = 3) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n = 6) являются одинаковыми (однако, как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}. В общем случае число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-й диагонали и n-й строки треугольника Паскаля. если кортежи имеют одинаковый состав, то такие картежи называются эквивалентными . На сколько классов эквивалентности тогда разбивается при этом вся совокупность кортежей длины из n элементов Эти классы и будут называться сочетаниями с повторениями из n элементов по k а их число обозначают .

Основные формулы:

Формула №1

при

Доказательство:

Вычисляя число размещений, мы получим пары, отличающиеся порядком элементов, Из двух элементов можно составить две перестановки упорядоченных пар, поэтому , так как число размещений , умноженному на число перестановок внутри группы . Для любого количество размещений из n элементов поk можно вычислить по формуле . Действительно из n элементов можно составить групп по k элементов, а в каждой группе можно выполнить перестановок. Таким образом число всех размещений равно произведению числа групп и числа перестановок внутри этих групп Отсюда следует что ч.т.д.

Формула № 2

Вывод формулы:

Формула №3

Доказательство: Любой состав кортежа длины k из n элементов имеет вид, — неотрицательные целые числа, сумма которых равна k. Заменяя каждое из чисел k, соответствующим количеством единиц о разделяя пулями единицы, отвечающие различным числам, получаем кортеж из n — 1 нулей и k единиц. При этом каждому составу отвечает одна и только одна запись с помощью нулей и единиц, а каждая такая запись задает один и только один состав. Поэтому число различных составов равно числу перестановок с повторениями из n — 1 нулей и k единиц, т. е. . Примеры задач:

Зaдача № 1Извесно, что имеется 13 983 810 различных способов заполнения карточки "Спортлото", а выиграли номера 1, 2, 3, 4, 5,6. Сколько лиц выиграли в эту игру?

Решение: Угадать все : удастся только 1так как =1Запишем пары, на первом месте которых стоит один из 6 заменяемых номеров, а на втором — тот номер, которым он заменяется.

(1,7) ,(1,8). . .(1,49)

(2,7) ,(2,8). . .(2,49)

…………………….

(6,7) ,(6,8) . . . (6,49)

Пара (1, 7) обозначает, что вместо правильной комбинации {1, 2, 3, 4, 5, 6} участник лотереи зачеркнул номера {7, 2, 3, 4, 5, 6}, угадав лишь 5 номеров. Из таблицы видно, что число возможностей ошибиться один и только один раз равно 6×43 = 258. Значит, 258 участников угадают 5 номеров. Таким же образом мы определяем, что 4 номера угадают =13 545 человек — сначала надо из 6 верных номеров выбрать какие-нибудь 2 (это делается способами), а затем заменить их парой номеров, выбранной из 43 несчастливых номеров (а это можно сделать способами).Комбинируя каждый способ выбора первой пары с каждым способом выбора заменяющей ее пары, тогда совпадут 3 цифры у одна цифра у человек и не одной цифры у .

Ответ угадает всё -1 угадает 5 цифр – 258, угадает 4цифры – 13 545, угадает 3- 246 820, угадают 2 цифры - человек, 1 цифру- , не угадает не одной .

Задача№2 Путник хочет попасть из пункта А в пункт В кратчайшим путем, т. е. двигаясь все время или "слева направо", или "снизу вверх". Сколькими путями он может добраться из А в В?

Решение. Ясно, что, каким бы путем ни шел путник, он пройдет через (n + k) перекрестков (считая точку А, но не считая точки В). На каждом перекрестке он может идти или направо, или вверх. В соответствии с этим все перекрестки делятся на два класса: "перекрестки направо" и "перекрестки вверх". При этом направо путник идет k раз, а вверх n раз. Значит, чтобы однозначно восстановить его путь, надо знать лишь те k случаев, когда он идет направо. Но их можно выбрать из общего числа (n + k) перекрестков способами. Поэтому число искомых путей равно Треугольник Паскаля

Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух, расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси^[1]. Имеет применение в теории вероятности и обладает занимательными свойствами.