1.Эл-ты комбинаторики.Размещ-я. Переста-новки. Сочетания.

ТВ-наука о вычислении вероят-тей случ.событий..Рассм-м эл-ты комбинаторики - раздел элем.мат-ки,изучающий вопрос кол-ва раз-лич.комбинаций,кот.можно составить при опред. условиях из бесконечн.множ-ва задан.объек-тов (х_1,х_2….х_n). Осн.правила комбинаторики: 1.правило произвед-я. Если компаненту х₁ карте-жа(х_1,х_2..х_n) можно выбрать n₁ способами,компаненту х₂ независимо от компанента х₁ выбрать n₂ спосо-бами ,компаненту х_к независимо от предыдущих компанентов выбрать n_к способом ,то картеж (х₁,х_2,…х_n)можно выбрать n_1,n_2..n_k. 2.правило суммы. Пусть из множ-ва А={а₁,а₂,..а_к} эл-т а₁ можно выбрать n₁ способом,а₂- n₂ способом, а_к- n_к.Тогда выбор одного из эл-тов множ-ва А а_1,а₂ или а_к можно сделать а₁₊а_2+…а_к. Картежем длины k составлен-м из эл-тов n-множ-ва Х наз-т размещением с повторе-нием из n эл-тов по k.Их число обозначают А¯^к_{n =} n*n …*n^к.Картежем длины k составлены из эл-тов n-множ-ва Х,у кот.все компаненты различны наз-ся размещением без повторений из эл-тов по k. Их число обознач-ся А^к_n.

А^к_n= n_*(n-1)*(n-2)…(n- k+1)= n_.!/_.(n- k)!

Размещением без повторений из n эл-тов по n эл-тов наз-ся перестановками из n эл-тов. Обозн-ся Р_n.Р_n=n! Подмнож-вом, сост-щим из k эл-тов взятые из множ-ва х наз-ся сочетаниями из n эл-тов по k и обознач-ся С^к _n. С^к _n= А^к_n/ Р_к= n !/(n- k)! k!

2. Испытания и события. Операции над событиями, их свойства. Испытанием назыв. эксперимент, который можно проводить в одинаковых условиях неопред. количество раз(подбрасывание монеты, подбрасывание игрального кубика). Случайным в теории вероятностей называют событие, которое при данном испытании, в данном опыте может либо произойти, либо не произойти и для которого имеется определенная вероятность его наступления. Вероятность случайного события A, обозначаемая P(A)– числовая мера степени возможности появления данного события при определенных условиях. При этом всегда 0<P(A)<1 Событие называется достоверным, если в результате опыта оно обязательно произойдет. Его вероятность равна единице.

Событие называется невозможным, если в результате опыта оно не может произойти; его вероятность равна нулю.

Суммой нескольких событий называется событие, заключающееся в появлении хотя бы одного из них. Несколько событий A₁,A₂,…A_n называются несовместимыми в данном опыте, если никакие два из них не могут появиться одновременно. Согласно теореме сложения вероятностей вероятность суммы несовместимых событий равна сумме вероятностей этих событий

Если в каком-то опыте может произойти либо событие A₁, либо событие A₂, то событие A₂ называют противоположным событию A₁, и обозначают , считая что:

3. Классическое определение вероятности. Статистическое и аксиоматическое определение вероятности. Классическое определение вероятности связано с определением благоприятствующего исхода. Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события. Вероятность события равна отношению числа равновозможных благоприятствующих элементарных исходов к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания: ,

где – число благоприятствующих событию исходов; – общее число возможных исходов.

Из определения вероятности события следует, что , поэтому всегда выполняются неравенства , т.е. вероятность любого события есть неотрицательное число, не превышающее единицы.

Простейшие свойства вероятностей: 1) ; 2) ; 3) ; 4) ;

Пусть произведено n-испытаний, при кот. соб-е А наступило К раз; 0≤k≤n, тогда отношение 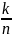=Wn наз-ся частотой случайного события А. А предел lim Wn наз-ся вероятностью соб. Р(А). Такое определение вер.соб. называется статистическим. Аксиоматическое определение вероятности. Вероятностью Р(А) случ-го соб-я А наз-ся числовая ф-ия, определённая на мно-ве всех соб. и удовлетв-ая 3 условиям: 1. Р(А)≥0; 2. 3.Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий: .

4.Теоремы сложения вероятности. Теорема 1. Вероятность суммы 2-ух событий ровна сумме вероятностей этих событий без вер-стей их совместного наступления. P(A+B)=P(A)+P(B)-P(A*B). Пусть число всех исходов n и даны 2 совместных события А и В, а число благо-ных исходов для А-k, В-l, A*B-q. P(A+B)=m/n. m=k+l-q. P(A+B)=(k+l-q)/n= P(A)+P(B)-P(A*B). Теорема 2. Вероятность суммы 2-ух несовместных событий равно сумме вер-стей этих событий. Р(А+В)=Р(А)+Р(В). Вследствие: сумма вероятностей событий А1 , А2….Аn, образующих в полную группу ровна 1. Теоремы умножения вероятностей. Вероятность события В при условии, что произошло событие А наз. условной вер-стью события В, обозн. РА(В) или РВ(А). Теорема 3. Вероятность произведения 2-ух событий ровна произведению вер-сти 1-го события на условную вер-сть 2-го события, при условии, что 1-я вер-сть произошла. Р(А*В)=Р(А)*РА(В), Р(А*В)=Р(В)*РВ(А). Два события наз.независимыми, если вер-сть наступления 1-го не зависит от того наступило ли другое событие или нет. РА(В)=Р(В). Следствие теоремы:вер-сть совместного наступления несколькихсобытий незав. совокупностей равна произведению вер-сти событий. Р(А1 *А2*…*Аn)=Р(А1 )*Р(А2)*…*Р(Аn)

5.Фор-ла полной вер-ти

Пусть соб-е А может наступить при усл. появл-я одного из событий Н_1,Н₂...Н_п обозначающих полную группу, тогда имеет место фор-ла полн. вер-ти

Р(А)=Р(Н₁)*Р_н1(А)+ Р(Н₂)*Р_н2(А)+…. Р(Н_п)*Р_нn(А)

Выведем эту формулу по условию событие АА может наступить, когда наступит одно из несовместных событий.

Другими словами, появл-е соб-я А означает осуществление одного из несовместных n-событий

Н₁*А,Н₂*А….Н_п*А

Т.об., что событие А= Н₁*А+Н₂*А+….Н_п*А

Р(А)=Р(Н₁*А)+Р(Н₂*А)+….Р(Н_п*А)

По теории умн-я вер-тей получим

Р(А)=Р(Н₁*А)+Р(Н₂*А)+….Р(Н_п*А)= Р(Н₁)*Р_н1(А)+ Р(Н₂)*Р_н2(А)+…. Р(Н_п)*Р_нп(А)-формула полной вероятности

6. При формуле полной вер-ти заранее известно, какое из событий Н₁,Н₂…H_n наступит, поэтому эти события называют гипотезами.

Формула Байеса позволяет уточнить гипотезы, при условии что событие А произойдет. Она имеет вид: Р_А(Нi)= (i= )

Выведем формулу Байеса

P(A*H_i)=P(A)*P_A(H_i)=P(H_i)*P_Hi(A)

Из последнего равенства можем выразить P_A(Hi)

P_A(Hi)= - формула Байеса

7.Повторение испытаний. Формула Бернули. Найвероятнейшее число появлений событий

Испытание Х_1,Х_2,…,Х_n наз-ся независимым,если исход каждого испытания не зависит от исходов всех предыдущих испытаний.Н-р:бросание монеты,игральной кости,выборочный контроль кач-ва прод-ции.

В схеме Якоба Бернулли рассматр-ся серия состоящая из n независимых испытаний Х_1,Х_2,…,Х_n, причем каждое из этих испытаний имеет лишь 2 исхода:а)событие А наступило-успех,б)событие А не наступило-неудача

Причем вер-ть успеха при одном испытании Р(А)=р(0≤р≤1) постоянна и не зависит от номера испытания. Числа n и p наз-ся параметрами схемы Бернулли.

В рамках схемы Бернулли у заданного числа m(0≤m≤n) опр-ть вер-тьP_n(m) того, что событие А в данной серии из n числа испытаний наступит точно m раз и имеет место формула Бернулли

P_n(m)=C_*p^mq^n-m

где q-вероят-ть неудачи q=1-p

Вероят-ть P_n(m) (m=0,n) наз-ся биномиальными в связи с тем, что правая часть фор-лы Бернулли совпадает с общим членом разложения Бинома-Ньютона:

(p+q)ⁿ=∑ C_*p^m_*q^n-m

^m=0

Очевидно, что сумма всех биномиальных вероятностей равна 1.

Отметим, что верот-ти m успехов при фиксированном m сначало растут до опред-го числа m₀, а потом убывают при уменьшении m от m₀ до n.

Оредел-ие: число успехов m₀, к которому при заданном фиксированном n соотв-ет max биномиальная вероят-ть Pn(m₀) наз-ся наиболее вероятным (наивероятнейшим) числом успехов.

Отметим,что наивероятнейшее число m₀ удовлетворяет системе неравенств: n*p-q≤m₀≤n*p+p, которое имеет одно решение: m=[np+p], если число np+p-не целое

Два решения:m₀=np+p

m₀₌np+p-1, если np+p-целое

8. Предельные теоремы для схемы Бернулли (Теорема Пуассона, локальная и интегральная теоремы Муавра-Лапласа). Функции Гаусса и Лапласа.

В случае, когда число испытаний велико, формулу Бернулли применять неудобно. Для больших существуют приближенные формулы. Точность этих формул увеличивается с возрастанием .

Теорема Пуассона: Предположим, что произведение np = является постоянной величиной, когда n неограниченно возрастает, тогда для любого фиксированного m и постоянного

На практике эта теорема применяется следующим образом. Если n велико, а p мало, , то 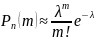– формула Пуассона.

Замечание: Если мало значение q₁ то по Пуассоновским приближениям можно воспользоваться для числа неудач.

Если же n достаточно велико, а p не слишком близко к нулю или единице, то имеет место теорема: Локальная теорема Муавра-Лапласа: , где ,

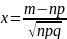а Функция называется ф-ей Гауса. Эта функция затабулирована – ф-ия Гауса чётная. При достаточно больших n вероятность того, что событие A в схеме Бернулли наступило не менее m₁ и не более m₂ раз в n испытаниях, при условии, что p не слишком близко к 0 или 1, вычисляется с помощью след. теоремы: Интегральная теорема Муавра-Лапласа: где , Ф-ия (x) называется ф-ией Лапласа,она нечётная, т.е. Ф(-x) = Ф(x)

Замечание: Иногда в литературе под ф-ей Лапласа подразумевается др. ф-ия

В этом случае интегральная ф-ла Лапласа