11. Дифракция света на круглом отверстии

Поместим на пути сферической волны непрозрачный экран с отверстиями.

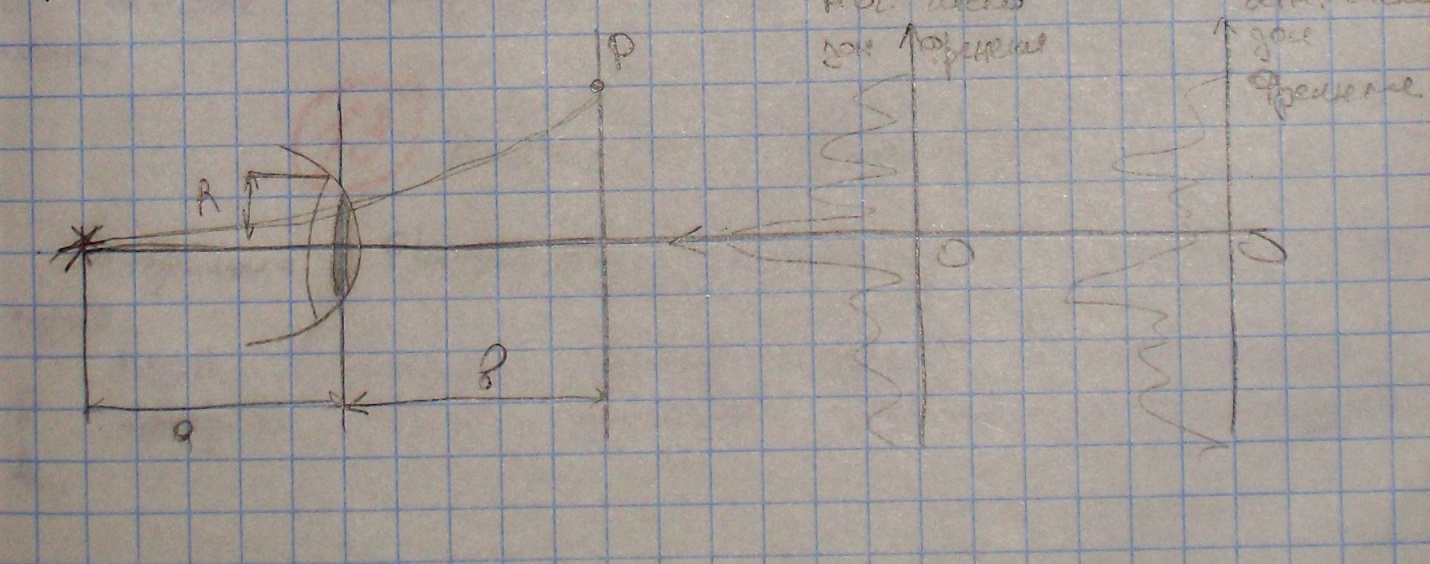
Если расстояния А и В точки, где радиус R будет удовлетворять радиусу зоны Френели:

то отверстие оставит открытых ровно и первых зон Френеля. Можно показать, что результирующая амплитуда в точке Р.

где плюс берется для нечетных М, а минус для четных М. Для малых М амплитуда А мало отличается от Ам, поэтому при нечетных м в точке Р амплитуда примерно равна А₁, а при четных м –нулю. Если убрать преграду, то амплитуда в точке Р будет равна А₁/2.

12. Дифракция света на диске

Поместим между источником света и экраном непрозрачный диск радиусом R.

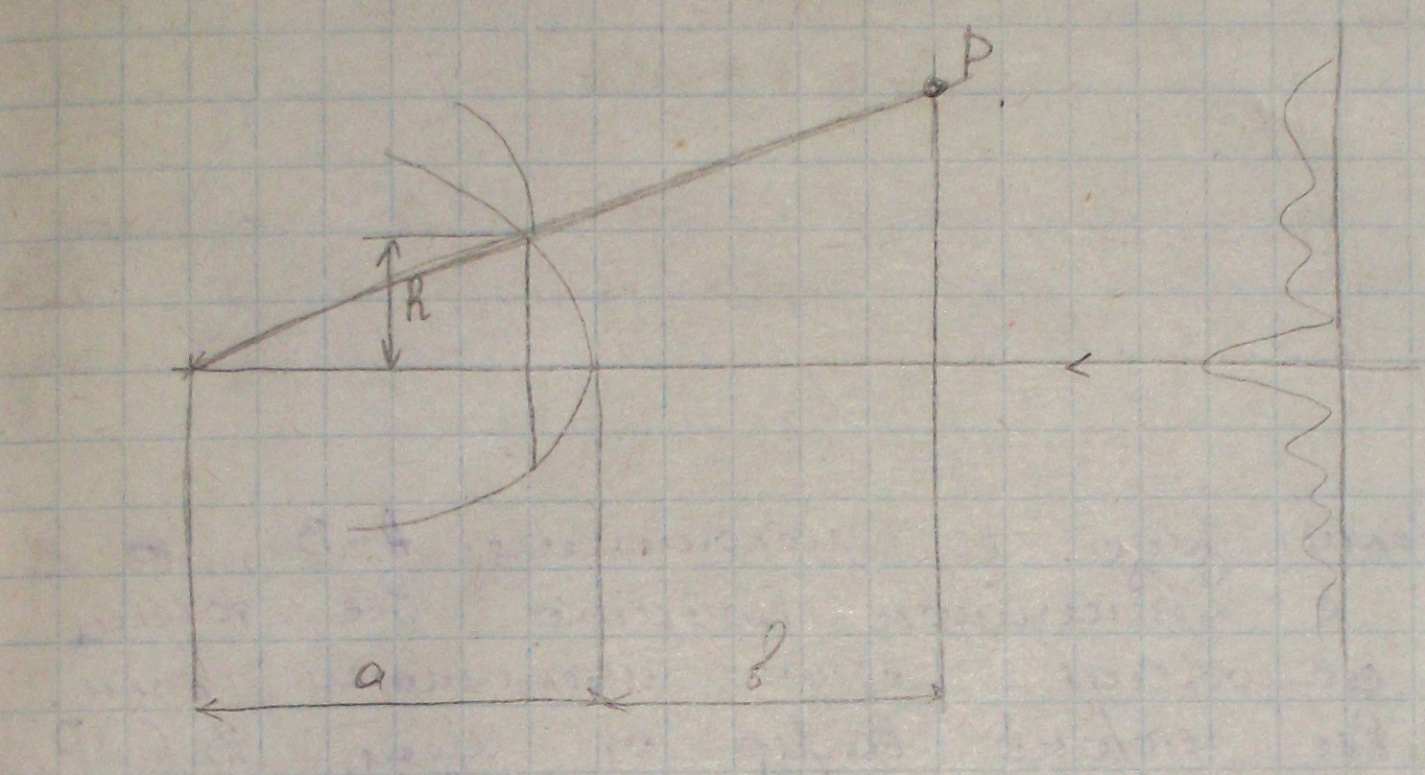
Если диск закроет m-первых зон Френеля, амплитуда в точке Р будет равна:

При небольшом числе закрытых зон Френеля амплитуда мало отличается от , по этому интенсивность почти такая же, как и в случае отсутствия диска, т.е. на экране будут светлые и темные концентрические кольца, в центре светлого пятна.

13. Дифракция Фраунгофера на одной щели

Дифракция Фраунгофера – дифракция в параллельных лучах. Пусть плоская волна подает перпендикулярно на экран, в которой имеется длинная узкая щель шириной А.

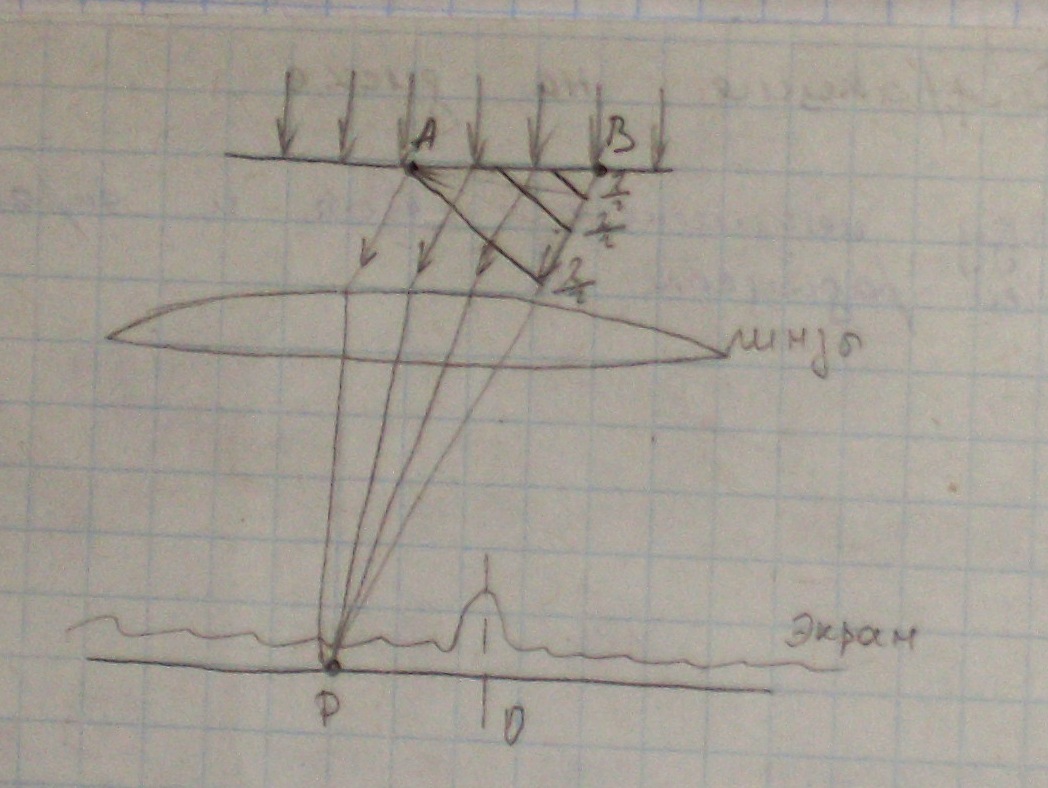
Когда фронт волны дойдет до положения А-В, то в соответствии с принципом Гюйгенса все точки отрезка А-В становятся новыми источниками волн, распространяющиеся во все стороны впереди от щели.

В точке Р экрана, расположенном в фональной плоскости линзы, будем наблюдать результат интерференции волн, распространяется под углом фи. Разность хода лучей возникает на пути от исходного фронта волны АВ до плоскости АС и различно для разных лучей. Применяем метод зон Френеля: для этого разделим линию ВС на ряд отрезков провода линии из концов этих отрезков параллельных АС, разобьем фронт волны на ряд полос одинаковой ширины – это и будут зоны Френеля соотв., что волны идущие от каждой из двух соседних зон приходят в точку В в противофазе и гасят друг друга. Число зон Френеля на отрезке ВС: ;

Если число зон Френеля будет четным, т.е. , то каждая пара соседних зон взаимно гасят друг друга и при данном угле на экране будет наблюдаться минимум: . Условие минимума при дифракции на щели.

Максимум будет наблюдаться при нечетном числе зон Френели: .

В центре будет наблюдаться центральный максимум.

С ростом м ширина зон Френели и интенсивность МАХ быстро уменьшается. Если на щели не монохроматический, а белый свет, то на экране будет наблюдаться белый центральный МАХ с радужной окраской по краям, все остальные интерференционные полосы цветные, т.к. МАХ и МИН одних и тех же порядков м соотв. в зависимости от длины волны разные углы дифракции и разные точки на экране.

14. Дифракционная решетка

Дифракционная решетка – оптический прибор, представляющий собой ряд параллельных щелей одинаковой ширины раздельными непрозрачными промежутками служащ. для разложения сета в спектр и увеличение интенсивности.

Период решетки (постоянная решетки)

К аждая точка щелей, до которой доходит плоский слой волны, становится источником вторичных волн. Эти вторичные волны начинают интерферировать между собой, тогда оптическая разность хода для лучей, идущих от соотв. точек:

В точку Р лучи приходя т со сдвигом фаз:

тогда условие главных максимумов дифракционной решетки:

При углах фи удовлетворяющих условию главных максимумов результирующая амплитуда в точке Р будет равна A=NA₁, где N – число щелей, а A₁– число колебаний от одной щели; тогда интенсивность дифракционной картины возрастает в N² раз по сравнению с дифракцией по одной щели.

Е сли на дифракционную решетку подать белый свет, то дифракция максимума для разных цветов разойдутся. Нулевой макс для всех длин волн будет совпадать при , то уже максимум первого порядка для фиолетового луча расположен ближе к центру чем для красного – между ними будут располагаться макс. промежуточных цветов – это и будет спектр первого порядка. Между спектрами различных порядков расположены темные зоны

= тк