Вопрос42. Вынужденное излучение. Оптические квантовые генераторы.

Вы́нужденное излуче́ние, индуци́рованное излучение — генерация нового фотона при переходе квантовой системы (атома, молекулы, ядра и т. д.) из возбуждённого в стабильное состояние (меньший энергетический уровень) под воздействием индуцирующего фотона, энергия которого была равна разности энергий уровней. Созданный фотон имеет ту же энергию, импульс, фазу и поляризацию, что и индуцирующий фотон (который при этом не поглощается). Оба фотона являются когерентными.

Введение. Теория Эйнштейна

Большой вклад в разработку вопроса о вынужденном излучении (испускании) внес А. Эйнштейн. Гипотеза Эйнштейна состоит в том, что под действием электромагнитного поля частоты ω молекула (атом) может:

• перейти с более низкого энергетического уровня 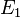на более высокий с поглощением фотона энергией (см. рис. 1a);

• перейти с более высокого энергетического уровня на более низкий с испусканием фотона энергией (см. рис. 1б);

• кроме того, как и в отсутствие возбуждающего поля, остаётся возможным самопроизвольный переход молекулы (атома) с верхнего на нижний уровень с испусканием фотона энергией (см. рис. 1в).

Первый процесс принято называть поглощением, второй — вынужденным (индуцированным) испусканием, третий — спонтанным испусканием. Скорость поглощения и вынужденного испускания фотона пропорциональна вероятности соответствующего перехода: и где  — коэффициенты Эйнштейна для поглощения и испускания,  — спектральная плотность излучения.

Число переходов с поглощением света выражается как

с испусканием света даётся выражением:

где  — коэффициент Эйнштейна, характеризующий вероятность спонтанного излучения, а  — число частиц в первом или во втором состоянии соответственно. Согласно принципу детального равновесия, при термодинамическом равновесии число квантов света при переходах должно равняться числу квантов испущенных в обратных переходах

Лазер – прибор для получения мощного электромагнитного излучения в оптическом диапазоне длин волн путем индуцированных переходов в квантовой системе.  Лазер обязательно имеет три основных компонента: 1) активную среду, в которой создаются состояния с инверсией населенностей; 2) систему накачки (устройство для создания инверсии в активной среде); 3) оптический резонатор (устройство, выделяющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок).

Оптический резонатор – система из 2 зеркал, имеющих общую оптическую ось, служащая для фокусировки вторичных фотонов.

В зависимости от природы активной среды различают такие типы лазеров: кристаллические, жидкостные, полупроводниковые, химические, газовые.Лазерное излучение обладает следующими свойствами:1. Временная и пространственная когерентность (2. Строгая монохроматичность (<10^–11 м).3. Большая плотность потока энергии. 4. Очень малое угловое расхождение в пучке.

43. Линейный гармонический осциллятор

Линейным гармоническим осциллятором называется частица массой m, которая колеблется с собственной частотой вдоль оси Ox под действием квазиупругой силы F, пропорциональной отклонению частицы от положения равновесия: F=-kx, где k-коэффициент квазиупругой силы. k=m . U(x)= - потенциальная энергия

Амплитуда малых колебаний гармонического осциллятора, в классической форме, определяется запасом его энергии.

з а пределы области [-a; a] частица выйти не может. Тогда вероятность обнаружить осциллятор на отрезке [x; dx]: (x)dx= .

В квантовой физике: + (w- ) =0; (x)= * * ( ), n=0,1,2,3…; ; ( )= * – полином Чербышева – Эрмита

Узел волновой функции – значения волновой функции =0.

Число узлов волновой функции равно квантовому числу n.

Собственное значение энергии нелинейного гармонического осциллятора:

=(n+ )h =(n+ ђ ; =

Энергия гармонического осциллятора – это совокупность равноотстоящих друг от друга энергетических уровней.

Наименьшая энергия, которую может иметь гармонический осциллятор называется нулевой энергией: = ђ

В классической физике и теории Планка считалось, что =0, при n=0, т.е. атомы не колеблются в близи абсолютного нуля.

В квантовой механике доказано, что нулевая энергия осциллятора не может быть от него отнята даже при T=0К. нулевые колебания характерны для любой системы частиц dx= dx, т.е. плотность вероятности отлична от нуля за пределами области |x| a. Этим объясняется возможность просачивания частиц, обладающих волновыми свойствами, через потенциальный барьер.