36. Стационарное уравнение Шрёдингера

Положение частиц в пространстве в данный момент времени определяется в квантовой механике заданием волновой функциии имеет зависимость от координат и времени φ(x,y,z,t).

Вероятность того, что частица находится в элементе объёма dω пропорциональна квадрату модуля волновой функции | элементу объёма dV: dω=| dV.

Величина квадрата модуля волновой функции(| ) есть плотность вероятности, т.е. задаёт вероятность преобразования частицы в данной точке пространства. – физический смысл волновой функции

Пси-функция( ) должна быть нормирована:

Условие нормирования указывает на то, что пребывание частицы где-либо в пространстве есть достоверное событие с вероятностью равной единице.

Условия, накладываемые на пси функцию:

1. Пси-ф-я должна быть конечной, однозначной и непрерывной

2. , , – первые частные производные должны быть непрерывны

3. Квадратичная функция от пси-модуля должна быть интегрируема

– конечен

В случае, когда пси-ф-я не зависит от времени, она удовлетворяет стационарному уравнению Шрёдингера: (w-U)Ψ=0,Δ= + + 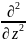, w-энергия частицы, U-потенциальная энергия частицы

Собственные функции – пси-ф-и, удовлетворяющие у-ю Шрёдингера при заданном виде потенциальной энергии: U=U(x,y,z).

Собственные значения энергии – энергии частицы, удовлетворяющие у-ю Шрёдингера.

Совокупность собственных энергий частицы образует энергетический спектр частицы.

В одномерном поле при свобод.движ.частицы, при постоянном U: + wΨ=0, v-const. =>Ψ=A*exp(- x)+B*exp( x), т.е. свободная частица в квантовой механике описывается плоской монохроматичной волной де Бройля с волновым числом k= . Если частица распространяется в положительном направлении оси Ox, то: = ; dω= V

37. Частица в одномерной потенциальной яме бесконечной глубины

Потенциальная яма – область пространства, в которой потенциальная энергия U частицы меньше некоторого значения . (U< )

U=U(x); ; U=0, если 0 ; , если x , тогда говорят, что яма имеет плоское дно.

+ wΨ=0. Ψ(0)= Ψ(L)=0, т.е. вероятность найти частицу вне области ямы (0 ) равна нулю => вне области =0.

Тогда решением уравнения Шрёдингера является ф-я:

, k= .

Из краевых условий следует, что A=0, B=0, sinkL=0. Sinkl=0, =nπ, n=1,2,3

= ; = ; => = , т.е. на длине потенциальной ямы должно укладываться целое число полуволн де Бройля. = .

= ; => – собственные значения энергии частицы в однородной потенциальной яме бесконечной глубины, представляет собой значения собственной энергии. уровни энергии, которые частица может иметь в потенциальной яме, n=1,2,3… – квантовое число

38. Соотношение неопределённостей Гайзенберга

Соотношением неопределённостей Гайзенберга называются неравенства вида: Δx* Δ ђ/2; Δy* Δ ђ/2; Δz* Δ ђ/2; ΔWΔt ђ, где Δy, Δx, Δя – интервалы координат, в которых может быть локализована частица (погрешность измерения координаты, неопределённость координаты частицы); Δ , Δ , Δ - интервалы проекции импульсов частицы на оси координат Ox, Oy, Oz (погрешность измерения импульсов частицы, неопределённость проекции импульса).

Соотношение неопределённостей показывают, что координата частицы и проекция её импульса не могут иметь значение в точности равные:

x и , y и , z и , W и t. Δ . Если x определена точно, то Δx=0 => Δ . Для энергии и времени то же самое.