19. Теорема о движении центра масс механической системы.
.
Уравнение движения механической системы:
;
;
.
Теорема:
Центр масс механической системы движется
как материальная точка, обладающая
массой механической системы, к которой
приложены все внешние силы, действующие
на данную механическую систему.
Следствия:
1. внутренние силы не влияют на движение механической системы.
2. если главный вектор всех внешних сил равен нулю, то центр масс находится в состоянии покоя или движется равномерно и прямолинейно.
3. если проекция главного вектора всех внешних сил на какую-либо ось равна нулю, то проекция центра масс неподвижна или движется равномерно и прямолинейно.
20. Моменты количества движения материальной точки относительно полюса и оси.
Момент
количества движения материальной точки
относительно полюса
- вектор численно равный произведению
количества движения на плечо d
(кратчайшее расстояние от полюса до
линии действия количества движения) и
направлен перпендикулярно плоскости,
проходящей через вектор количества
движения и полюс, в сторону, откуда
вращение вектора вокруг полюса видно
против часовой стрелки:
,
где r
- расстояние от полюса до материальной
точки.
Проекция
момента количества движения материальной
точки относительно полюса на ось,
проходящую через этот полюс равна
моменту количества движения точки
относительно этой оси:
,
где k
- единичный орт оси z.
Теорема об изменении момента количества движения материальной точки.
;
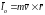взяв производную по времени от обоих
частей уравнения получим:
,
итак:
.
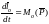Теорема: векторная производная по времени от момента количества движения материальной точки относительно полюса равна вектору момента силы, действующей на точку относительно того же центра.
Следствия:
1. если линия действия силы проходит через полюс. То момент количества движения относительно этого полюса постоянный;
2. если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси постоянный.
21. Кинетический момент механической системы относительно центра и оси.
Кинетический
момент относительно полюса
- главный момент количества движения
механической системы относительно
полюса - вектор, равный геометрической
сумме момента количества движения всех
точек системы относительно того же
полюса:
Кинетический
момент относительно оси
- скаляр, равный алгебраической сумме
моментов количеств движения всех точек
системы относительно той же оси:
Кинетический
момент вращающегося твердого тела
относительно оси вращения равен
произведению угловой скорости на момент
инерции тела относительно оси вращения:
;
22. Теорема об изменении кинетического момента механической системы.
Теорема: векторная производная по времени от кинетического момента механической системы относительно полюса геометрически равна главному моменту все внешних сил, действующих на механическую систему.
Следствия:
1. внутренние силы не влияют на изменение кинетического момента;
2. если главный момент все внешних сил относительно полюса равен нулю, то кинетический момент относительно этого полюса постоянный;
3. если главный момент все внешних сил относительно оси равен нулю, то кинетический момент относительно этой оси постоянный.