1. Две основные задачи динамики точки.

1. Зная массу материальной точки и уравнение ее движения определить модуль и направление равнодействующей силы, под действием которой точка движется.

2. Зная силы, действующие на материальную точку, ее массу и начальные условия движения определить траекторию.

2. Дифференциальные уравнения движения свободной материальной точки в декартовых координатах.

Метод кинетостатики: если к движущейся под действием сил точке приложить силу инерции, то геометрическая сумма всех сил будет равна нулю: , где Ф - сила инерции.

Так как: , то проектируя на ось координат получаю: , так как: то аналогично для y и z получаю:

4. Динамическая теорема Кориолиса. Переносная и Кориолисова силы инерции.

Переносная сила инерции точки в ее относительном движении направлена противоположно вектору переносного ускорения точки и численно ровно произведению массы точки, на величину переносного ускорения точки: -ma_е=Ф_е - сила инерции

Сила инерции Кориолиса, направлена в сторону противоположную ускорению Кориолиса, и ровно произведению массы точки на величину ускорения Кориолиса: -ma_k=Ф_k – Кориолисова сила инерции. ma_r= - динамическая теорема Кориолиса

5. Дифференциальные уравнения относительного движения материальной точки.

, подставляя в основное уравнение динамики: , обозначая переносную и Кориолисову силы инерции: 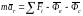. В проекциях на координатные оси:

6. Свободные колебания материальной точки

- диф. уравнение свободных гармонич. колебаний

x=x₀coskt+ sinkt – 1-я форма уравнения гармонич. колебаний

x=asin(kt+α) – 2-я форма уравнения гармонич. колебаний

k= – круговая частота колебаний

T= – период

a= – амплитуда колебаний

7. Затухающие колебания мат. точки

Затухающие колебания происходят в том случае, когда на точку, кроме восстанавливающей силы действует сила сопротивления.

R=-µv µ - коэффициент сопротивления среды

– диф. уравнение затухающих колебаний

n= - частота затухающих колебаний

8. Затухающие колебания в случае малого сопротивления

k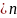

k₁= - частота

- 1- я форма ур. зат. колебаний - 2- я форма ур. зат. колебаний

Т= – период

Д=- логарифмический дикримент затухания

9. Затухающие колебания в случае большого сопротивления

n

k₁= - частота

– ур-е затух. колебаний большого сопрот.

случай апериодического движения

10. Вынужденные колебания без учета сопротивления среды

Такие колебания происходят, если на точку, кроме восстанавливающей силы действует вынуждающая сила, изменяющаяся по гармоническому закону: H

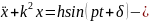диф. ур-е. вынужд. колеб. без сопр. сред

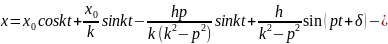1-я форма ур-я.

2-я форма ур-я.

удельная амплитуда

A= амплитуда вынужденных колебаний

11. Случай резонанса

k=p

ур-е. колеб. р.

12. Вынужденные колебания с учетом сопротивления среды

Такие колебания происходят, если на точку, кроме восстанавливающей и вынуждающей силы действует сила сопротивления:

R=-µv µ - коэффициент сопротивления среды

диф. ур-е. вынужд. колеб. с сопр. среды

- амплитуда вынужденных колебаний с сопр.

- ур-е вынужденных колеб.

13. Координаты центра масс системы материальных точек. Силы, действующие на точки механической системы.

Механическая система материальных точек - совокупность точек, в которой положение и движение каждой зависит от остальных. Система с кинематическими ограничениями - несвободная. Масса механической системы - арифметическая сумма масс всех ее точек. Центр масс - геометрическая точка, положение которой определяется уравнениями: Задаваемые силы и реакции связи;

Внешние силы - силы, с которыми на механическую систему действуют другие тела, не входящие в нее.

Внутренние силы - силы взаимодействия точек системы. Свойства внутренних сил:

1. главный вектор внутренних сил равен нулю;

2. главный вектор момент внутренних сил относительно любого неподвижного центра равен нулю