Решение

Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 4-5-6. Разобьем отрезок интегрирования, например, на те же 5 частей.

И шаг, естественно, тоже известен:

В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):

i	0	1	2	3	4	5
x_i	4	5	6	7	8	9
f(x_i)	2	1.809	1.689	1.607	1.546	1.5

В результате:

После первичного результата количество отрезков удваивают. В данном случае необходимо провести разбиение на 10 отрезков.

Для n= 10 формула трапеций приобретает следующий вид:

Вычислим шаг разбиения:

Результаты расчётов сведём в таблицу:

i	0	1	2	3	4	5
x_i	4	4.5	5	5.5	6	6.5
f(x_i)	2	1.891	1.809	1.743	1.689	1.645
i	6	7	8	9	10
x_i	7	7.5	8	8.5	9
f(x_i)	1.607	1.575	1.546	1.522	1.5

В результате:

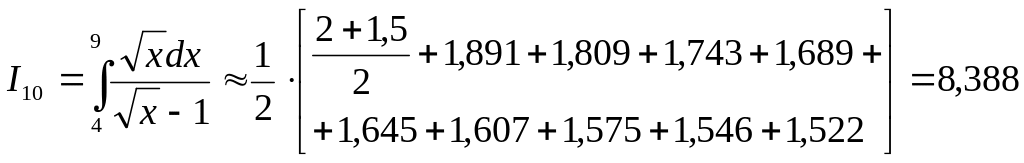
Теперь рассчитаем, на сколько улучшился результат:

Полученная оценка погрешности меньше, чем требуемая точность.

Ответ:

б) Используя обобщенную формулу Симпсона составить таблицу значений функции, заданной в виде интеграла с переменным верхним пределом.

Решение

Если функция у = f(x) интегрируема на отрезке , то функция Ф(х) непрерывна на этом отрезке.

Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела. т.е.

Сначала отрезок интегрирования разбивается на 8 отрезков. Разобьем отрезок интегрирования, например, на те же 8 частей.