Решение
Строим график
функции
x |
y |
-15 |
-3563 |
-14 |
-2920 |
-13 |
-2361 |
-12 |
-1880 |
-11 |
-1471 |
-10 |
-1128 |
-9 |
-845 |
-8 |
-616 |
-7 |
-435 |
-6 |
-296 |
-5 |
-193 |
-4 |
-120 |
-3 |
-71 |
-2 |
-40 |
-1 |
-21 |
0 |
-8 |
1 |
5 |
2 |
24 |
3 |
55 |
4 |
104 |
5 |
177 |
6 |
280 |
7 |
419 |
8 |
600 |
9 |
829 |
10 |
1112 |
11 |
1455 |
12 |
1864 |
13 |
2345 |
14 |
2904 |
15 |
3547 |
Рис. 1. График функции
Анализируя полученное изображение графика, можно сказать, что уравнение имеет один корень – это видно из пересечения графика функции с осью OX. Можно выбрать отрезок, содержащий данный корень: [0,5;1] – отрезок изоляции.
Для подтверждения
полученных данных, можно решить эту же
задачу вторым способом. Для этого
необходимо уравнение
преобразовать к виду:
.
Затем следует каждую часть уравнения
рассмотреть как отдельную функцию. Т.
е.
x |
y1 |
y2 |
-15 |
-3375 |
188 |
-14 |
-2744 |
176 |
-13 |
-2197 |
164 |
-12 |
-1728 |
152 |
-11 |
-1331 |
140 |
-10 |
-1000 |
128 |
-9 |
-729 |
116 |
-8 |
-512 |
104 |
-7 |
-343 |
92 |
-6 |
-216 |
80 |
-5 |
-125 |
68 |
-4 |
-64 |
56 |
-3 |
-27 |
44 |
-2 |
-8 |
32 |
-1 |
-1 |
20 |
0 |
0 |
8 |
1 |
1 |
-4 |
2 |
8 |
-16 |
3 |
27 |
-28 |
4 |
64 |
-40 |
5 |
125 |
-52 |
6 |
216 |
-64 |
7 |
343 |
-76 |
8 |
512 |
-88 |
9 |
729 |
-100 |
10 |
1000 |
-112 |
11 |
1331 |
-124 |
12 |
1728 |
-136 |
13 |
2197 |
-148 |
14 |
2744 |
-160 |
15 |
3375 |
-172 |
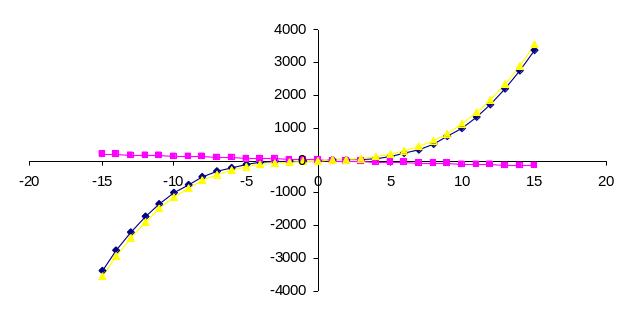
Рис. 2. Наложение искомых функций
Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок изоляции [0,5;1], что и при решении задачи первым способом.
Сделаем крупнее масштаб.
Рис. 3. Увеличенный масштаб
При увеличенном масштабе, корень уравнения х=0,644.
Метод бисекции
(метод половинного деления).
Пусть мы отделили корень на отрезке
.
Разделим отрезок
пополам точкой
.
Если
,
то возможны два случая: либо
меняет знак на отрезке
,
либо на отрезке
.
Выбираем в каждом случае тот из отрезков,
на котором функция меняет знак, и
продолжаем процесс деления до тех пор,
пока
,
где
-
точность.
Таким, образом х=0,644
Строим график
функции
x |
y |
-15 |
-0,99118 |
-14 |
-0,98438 |
-13 |
-0,97253 |
-12 |
-0,95215 |
-11 |
-0,91748 |
-10 |
-0,85938 |
-9 |
-0,76367 |
-8 |
-0,60938 |
-7 |
-0,36719 |
-6 |
0 |
-5 |
0,53125 |
-4 |
1,25 |
-3 |
2,125 |
-2 |
3 |
-1 |
3,5 |
0 |
3 |
1 |
1 |
2 |
-1 |
3 |
7 |
4 |
63 |
5 |
287 |
6 |
1023 |
7 |
3199 |
8 |
9215 |
9 |
25087 |
10 |
65535 |
11 |
165887 |
12 |
409599 |
13 |
991231 |
14 |
2359295 |
15 |
5537791 |
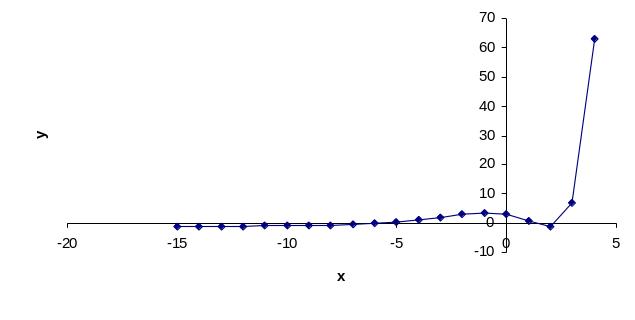
Рис. 1. График функции
Анализируя полученное изображение графика, можно сказать, что уравнение имеет три кореня – это видно из пересечения графика функции с осью OX. Можно выбрать несколько отрезков, содержащий данный корень: [-17,5;-16,5], [-6,5;-5,5], [1,5;2,5] – отрезки изоляции.
Для подтверждения
полученных данных, можно решить эту же
задачу вторым способом. Для этого
необходимо уравнение
преобразовать к виду:
.
Затем следует каждую часть уравнения
рассмотреть как отдельную функцию. Т.
е.
x |
y1 |
y2 |
-15 |
3,05176E-05 |
0,00346 |
-14 |
6,10352E-05 |
0,003906 |
-13 |
0,00012207 |
0,004444 |
-12 |
0,000244141 |
0,005102 |
-11 |
0,000488281 |
0,005917 |
-10 |
0,000976563 |
0,006944 |
-9 |
0,001953125 |
0,008264 |
-8 |
0,00390625 |
0,01 |
-7 |
0,0078125 |
0,012346 |
-6 |
0,015625 |
0,015625 |
-5 |
0,03125 |
0,020408 |
-4 |
0,0625 |
0,027778 |
-3 |
0,125 |
0,04 |
-2 |
0,25 |
0,0625 |
-1 |
0,5 |
0,111111 |
0 |
1 |
0,25 |
1 |
2 |
1 |
2 |
4 |
|
3 |
8 |
1 |
4 |
16 |
0,25 |
5 |
32 |
0,111111 |
6 |
64 |
0,0625 |
7 |
128 |
0,04 |
8 |
256 |
0,027778 |
9 |
512 |
0,020408 |
10 |
1024 |
0,015625 |
11 |
2048 |
0,012346 |
12 |
4096 |
0,01 |
13 |
8192 |
0,008264 |
14 |
16384 |
0,006944 |
15 |
32768 |
0,005917 |
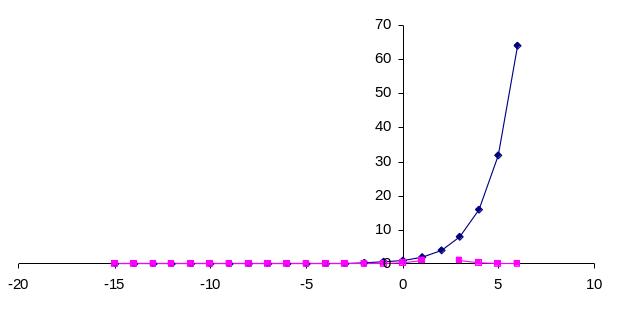
Рис. 2. Наложение искомых функций
Анализируя полученный результат, можно сказать, что точки пересечения двух графиков попадает на те же самые отрезки изоляции [-17,5;-16,5], [-6,5;-5,5], [1,5;2,5] – отрезки изоляции, что и при решении задачи первым способом.
Сделаем крупнее масштаб.
Рис. 3. Увеличенный масштаб
При увеличенном масштабе, корень уравнения х=0,644.
Метод бисекции (метод половинного деления). Пусть мы отделили корень на отрезке . Разделим отрезок пополам точкой . Если , то возможны два случая: либо меняет знак на отрезке , либо на отрезке . Выбираем в каждом случае тот из отрезков, на котором функция меняет знак, и продолжаем процесс деления до тех пор, пока , где - точность.
Таким, образом х=-6
Задание 3
а) Используя обобщенные формулы трапеций и Симпсона вычислить определенные интегралы с заданной точностью. Проверку достижения требуемой точности проводить по правилу Рунге.
