10. Закон сохранения механической энергии, его связь с однородностью времени.

Закон сохранения энергии в механике: механическая энергия замкнутой консервативной системы не изменяется в процессе ее движения:

W = W_k + W_p = const.

закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система

10. Кинематика вращательного движения: вектор элементарного угла поворота, угловая скорость, угловое ускорение. Связь угловых и линейных характеристик при вращательном движении.

Элементарный поворот dφ – аксиальный вектор, модуль которого равен углу поворота dφ, а направление вдоль оси вращения ОО' (см. рис. 1.4) определяется правилом правого винта.

Угловая скорость ω – аксиальный вектор, определяемый производной вектора поворота по времени:

ω=dφ/dt=φ'

Угловое ускорение β – аксиальный вектор, определяемый производной вектора угловой скорости по времени:

β=dω/dt=d²φ/dt²=ω'=φ''

10. Момент инерции (материальной точки, системы материальных точек, твердого тела). Моменты инерции тел правильной геометрической формы относительно оси, проходящей через центр масс. Теорема Штейнера.

Моментом инерции материальной точки относительно оси вращения называется физическая величина, численно равная произведению массы точки на квадрат расстояния точки до оси вращения.

I = mr²

Моментом инерции механической системы относительно неподвижной оси называется физическая величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до оси вращения.

Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси. 

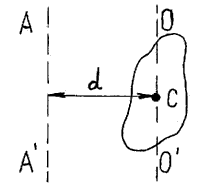
Момент инерции тела относительно произвольной оси АА' равен сумме момента инерции тела относительно оси ОО', проходящей через центр масс тела и параллельной данной оси АА', и произведения массы тела как целого на квадрат расстояния d между осями АА' и ОО' 

10. Момент силы (относительно неподвижной точки, относительно неподвижной оси).

Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы.

Если имеется материальная точка  , к которой приложена сила  , то момент силы относительно точки   равен векторному произведению радиус-вектора  , соединяющего точки   и  , на вектор силы  :

.

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

10. Момент импульса материальной точки и системы материальных точек (относительно неподвижной точки, относительно неподвижной оси).

Момент импульса материальной точки относительно точки O определяется векторным произведением , где   — радиус-вектор, проведенный из точки O,   — импульс материальной точки. Момент импульса материальной точки относительно неподвижной оси    равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса    не зависит от положения точки O на оси z.