2; величина лага k соответствует двум неделям). В то же время для второго вида– L. dominicanus – подобная зависимость не наблюдается.

Эффективным способом визуальной оценки пространственной анизотропии изучаемого явления является построение поверхности вариограммы, пример которой представлен для распределения численности моллюскаB. cylindrica на пробном участке

парка в г. Днепропетровске (Шитиков, Розенберг, 2014):

С доступным математическим описанием этого метода можно ознакомиться, например, на сайте dvseisgeo.ru. Функции для построения вариограмм входят в состав нескольких пакетов для R (например, функция Variogram() из стандартного R-пакета nlme; функция variog() из пакета geoR; функция variogram() из пакета gstat).

Что же делать, если рассмотренный выше разведочный анализ данных выявил некоторые отклонения от пунктов представленного протокола? Ответ таков: использовать

байесовских методов, робастных форм регрессии, обобщенных линейных и аддитивных моделей и др.

6.2.Линейные модели дисперсионного анализа

Вразделе 5.5, который представлял собой введение в дисперсионный анализ (ANOVA), мы упомянули о том, что в R этот анализ можно выполнить как с помощью функции aov(), так и lm(), которая предназначена для построения линейных регрессионных моделей. Напомним, что под статистическими моделями понимаются математические выражения, описывающие связь между анализируемыми случайными переменными. Модель считается линейной (или обладает свойством суперпозиции), если отклик системы на сумму независимых воздействующих факторов равен сумме откликов на каждое воздействие.

184

Суть "классического" однофакторного дисперсионного анализа мы рассматривали на примере эксперимента (Maindonald, Braun, 2010), в котором томаты выращивали при трех разных экспериментальных условиях: на воде, в среде с добавлением удобрения, а также в среде с добавлением удобрения и гербицида. В конце эксперимента был измерен вес растений из этих трех групп.

Мы выяснили, что каждое измеренное значение веса растений можно разложить на следующие составляющие:

вычисленного по всем значениям веса растений), а (xij - xi· ) – отклонения отдельных наблюдений от среднего значения группы, к которой они принадлежат.

Используя эти отклонения, а также учитывая число анализируемых групп и число наблюдений в каждой группе, мы далее рассчитали меж- и внутригрупповую дисперсии и сравнили их при помощи F-критерия Фишера. Исходя из величины полученного критерия, был сделан вывод, что нулевую гипотезу об отсутствии разницы между групповыми средними значениями массы растений отклонять нельзя.

Уравнение (1) для однофакторного дисперсионного анализа можно записать в более простом виде:

где yij – вес растения j из экспериментальной группыi, μ – среднее значение веса всех задействованных в эксперименте растений, αi – разность между μ и средним значением растений в группе i, a eij – это остатки, отражающие отклонения отдельных наблюдений в группе i от среднего значения этой группы. Предполагается, что остатки имеют нормальное распределение со средним значением 0 и стандартным отклонением σ, причем это стандартное отклонение одинаково во всех группах.

моделью, в которой переменная-отклик аддитивна относительно эффектов, оказываемых предикторами (т.е. независимыми переменными по правую сторону равенства):

где yi – это i-е значение зависимойколичественной переменной y; xi – значение количественного предиктора x, соответствующее i-тому значению y; β0 – значение, которое принимает y при x = 0 (геометрически, это точка, в которой линия регрессии пересекает ось Y; отсюда англ. термин для этого коэффициента– intercept, что значит "пересечение"); β1 – коэффициент регрессии, который показывает, насколько изменяется y при изменении x на одну единицу; ei – это остатки, т.е. разница между наблюдаемыми значениями yi и средними значениями, предсказанными моделью для каждого xi.

Наиболее важные отличия между уравнениями (2) и (3) заключаются в следующем:

°В обоих случаях зависимая переменнаяy является количественной. Однако в

взаимосвязи между предиктором и независимой переменной в регрессионной модели определяется коэффициентом регрессии β1 в уравнении(3). В дисперсионном анализе размер эффекта изучаемого фактора(т.е. степень отклонения групповой средней от общего среднего значения) выражен при помощи разностей αi.

185

К сожалению, с моделью в уравнении(2) имеется одна проблема– не все ее параметры идентифицируемы. Это значит, что существует бесконечное множество возможных (неуникальных) значений параметров модели. Например, если мы добавим к μ 2.5 (или любую другую константу) и соответственно вычтем 2.5 из каждого αi, то получим точно те же значенияyij. Однако проблему неидентифицируемости можно легко обойти, наложив определенные ограничения на параметры модели.

При работе с категориальными предикторами(факторами) возможны несколько разных подходов к наложению подобных ограничений– см., например, (Faraway, 2009, с. 191-192). Во многих статистических программах, включая R, величину эффекта для первого уровня анализируемого фактора("базового" уровня; англ. reference level или baseline level) по умолчанию принимают равной0: α1 = 0. Тогда μ будет представлять собой среднее значение зависимой переменной для базового уровня фактора(например, в контрольной группе какого-либо эксперимента), тогда как αi для i ≠ 1 будут отражать разницу между средним значением базового уровня и средними значениями остальных уровней. Используя этот подход, мы можем переписать уравнение (2) в виде регрессионного уравнения следующим образом:

где β0 – среднее значение зависимой переменной для базового уровня изучаемого фактора (например, в контрольной группе); β1 … βk-1 – коэффициенты, отражающие разницу между средним значением базового уровня и средними значениями остальных уровней; ei – остатки.

Ключевой момент для понимания здесь состоит в ,томчто уровни изучаемого фактора (всего имеется k таких уровней) закодированы при помощи дополнительной переменной-индикатора x (англ. dummy variable, дословно "переменная-пустышка"), которая может принимать только два значения– 0 или 1, в зависимости от того, к какому уровню принадлежит конкретное наблюдениеyi. Например, если наблюдение y3 принадлежит к уровню x1, тогда x1 в уравнении (4) примет значение 1, а x2…xk-1 все будут равны 0, и, следовательно, для наблюдения y3 регрессионное уравнение примет вид:

y3 = β0 + β1×1 + e3 = β0 + β1 + e3

Уравнение (4) как раз и описывает ту линейную модель, которая рассчитывается в R при выполнении однофакторного дисперсионного анализа с помощью функцииlm(). Посмотрим, как это всё работает, вернувшись к примеру с растениями томатов, которые выращивали при разных экспериментальных условиях.

# Создадим таблицу с данными: tomato <-

data.frame(weight=

c(1.5, 1.9, 1.3, 1.5, 2.4, 1.5, # water 1.5, 1.2, 1.2, 2.1, 2.9, 1.6, # nutrient

1.9, 1.6, 0.8, 1.15, 0.9, 1.6), # nutrient+24D trt = rep(c("Water", "Nutrient", "Nutrient+24D"),

c(6, 6, 6)))

уровень из этого списка(например, в нашем случае это был бы уровеньNutrient). Задать базовый уровень фактора в R позволяет функция relevel():

186

# Автоматически R выберет Nutrient в качестве базового уровня: levels(tomato$trt)

[1] "Nutrient" "Nutrient+24D" "Water"

# Изменим базовый уровень на Water:

tomato$trt <- relevel(tomato$trt, ref = "Water") levels(tomato$trt)

#Сохраним модель в виде объекта с именем М:

M <- lm(weight ~ trt, data = tomato)

#Просмотрим результаты вычислений:

Residual standard error: 0.5107 on 15 degrees of freedom Multiple R-squared: 0.1381, Adjusted R-squared: 0.02321 F-statistic: 1.202 on 2 and 15 DF, p-value: 0.328

коэффициентов мы можем легко проверить, рассчитав средние значения для каждой экспериментальной группы:

187

tapply(tomato$weight, tomato$trt, mean)

В столбцах Std. Error, t value и Pr(>|t|) представлены стандартные ошибки рассчитанных коэффициентов, значения t-критерия Cтьюдента, который используется для проверки гипотезы о равенстве коэффициента нулю, и р-значения для каждого t-критерия соответственно. Как видим, ни один из исследованных уровней фактора "условия выращивания" не отличается от базового уровня по среднему значению веса растений – в обоих случаяхр-значения регрессионных коэффициентов оказались >0.05, что указывает на то, что наблюдаемое их отличие от нуля с большой долей вероятности является случайным. Другими словами: исследованные условия выращивания в среднем не оказали никакого влияния на вес растений по сравнению с растениями, выращенными на воде.

Далее в таблице с результатами анализа мы видим:

°Residual standard error – оценка стандартного отклонения остатков. Вспомним: предполагается, что остатки имеют нормальное распределение со средним значением 0 и стандартным отклонением σ. В данной строке результатов анализа как раз и приводится оценка значения σ.

°Multiple R-squared и Adjusted R-squared – коэффициент детерминации

икоэффициент детерминации с поправкой на число параметров модели соответственно.

°F-statistic – значение критерия Фишера, при помощи которого проверяется

нулевая гипотеза о том, что все коэффициенты истинной модели (в нашем случае β1 и β2) равны 0.

Значение F-критерия для линейных моделей рассчитывается как отношение дисперсии в данных, "объясненной" параметрами модели, к дисперсии остатков(т.е., части общей дисперсии, которую модель "не объясняет"). Это легко увидеть, используя объект M как параметр функции anova() (не путать с aov()):

anova(M)

Analysis of Variance Table Response: weight

Df Sum Sq Mean Sq F value Pr(>F) trt 2 0.6269 0.31347 1.2019 0.328 Residuals 15 3.9121 0.26081

использованием функции aov().

Идентичность результатов не удивительна, поскольку, в конечном счете, мы в обоих случаях оцениваем одни и те же наиболее важные величины – дисперсию в данных, ассоциированную с действием изучаемого фактора, и остаточную дисперсию, которую мы не можем приписать действию этого фактора. С точки зрения программного кода, aov() является лишь "функцией-упаковщиком" (англ. wrapper function), назначение которой сводится к вызову функции lm(). Различие между этим двумя функциями состоит только в том, как получаемые с их помощью результаты выводятся при подаче наprint() и

summary(). В случае с aov() результаты выводятся в виде классической таблицы дисперсионного анализа, а не в виде списка с коэффициентами линейной модели.

Следует также отметить, что функция aov() предназначена для анализа сбалансированных наборов данных, т.е. таких ситуаций, когда имеется одинаковое число

188

наблюдений для каждого уровня изучаемого фактора. Если условие сбалансированности не выполняется, следует использовать функциюlm() (пробнее см. справочный файл, доступный по команде ?lm).

Generalized Linear Models). Понимание концепции ОЛМ очень важно для осмысленного использования lm() и других функцийR, позволяющих создавать линейные модели. Поэтому стоит остановиться на ОЛМ более подробно.

Общую линейную модель можно выразить в матричном виде следующим образом:

где Y – многомерная матрица предсказываемых моделью значений; X – матрица модели (model matrix) или матрица плана (design matrix), которая содержит значения включенных в модель предикторов; B – матрица параметров модели, которые оцениваются на основе имеющихся данных, а U – матрица остатков модели.

В случае однофакторного дисперсионного анализа мы имеем дело с одномерной

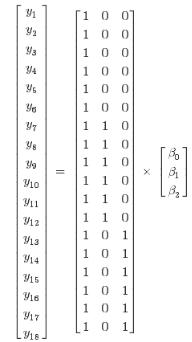
переписать уравнение (4) в матричной форме, следуя концепции ОЛМ (уравнение 6):

В этом уравнении по левую сторону от знака"=" мы видим все измеренные значения веса растений из соответствующих экспериментальных групп(сначала идут 6 значений из контрольной группы, затем 6 значений из группы Nutrient и, наконец, 6 значений из группы Nurtient+24D).

Сразу после знака"=" представлена матрица плана модели размером18´3. Как было отмечено выше, размерность этой матрицы определяется объемом наблюдений(n = 18) и числом подлежащих оценке параметров модели(в нашем случае m = 3). Матрица

189

модели содержит значения переменной-индикатораx (англ. dummy variable), которая принимает только два значения– 0 и 1, и служит для обозначения принадлежности каждого наблюдения yi к той или иной экспериментальной группе. Просмотреть матрицу

той или иной подогнанной линейной модели можно с использованием функции model.matrix(), которая для созданной нами выше модели M дает матрицу, в точности соответствующую матрице модели из уравнения (6):

"contr.treatment", мы расскажем в следующем разделе.

Матрица модели умножается на матрицу с параметрами ,моделикоторая в рассматриваемом примере представлена вектором из 3 величин – β0, β1 и β2, отражающих разницу между средним значением веса растений в контрольной группе и средними значениями в других группах. Оценки этих параметров модели, полученные выше с

группы. Отсюда мы и получаем то, что называется остатками – это разности между наблюдаемыми и предсказанными значениями, которые не могут быть объяснены включенными в модель предикторами.

Согласно правилам умножения матриц, каждое значение yi получается путем поэлементного произведения чисел из i-й строки матрицы модели на вектор, содержащий параметры модели. Например, прогнозируемый вес растения для первого значения из

уравнении (5).

Универсальность матричной формы состоит еще и в ,томчто матрица модели может включать значения предикторов любого типа– как количественных, так и

190