12. Парал соединение r, l, c. Треугольники токов,проводимостей, мощностей.

На рис. 3.12 представлена параллельная цепь из элементов R, L, C и приборов электромагнитной системы, измеряющих действующие значения величин. Анализ цепи произведем комплексным методом. П задано напряжение , т.е. .

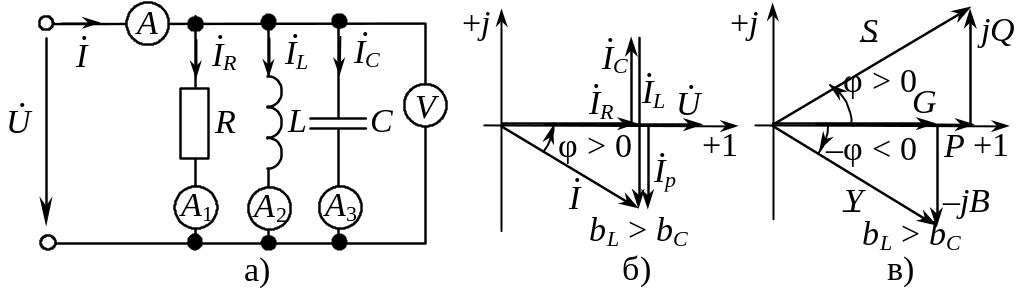
Рис. 3.12. Цепь с параллельным соединением элементов (а)), векторная диаграмма токов (б)), проводимостей и мощностей (в)) при b_L>b_C

Опред комплексные проводимости ветвей: ; ;

комплексная проводим цепи

где  – полная проводимость цепи;  – сдвиг фаз между входными напряжением и током; B=B_L–B_C – реактивная проводимость цепи.По закону Ома находим комплексный входной ток: ,где I=YU – измеряемое амперметром А действующее значение входного тока. В схеме замещения на рис. 3.12а все проводники идеальные, поэтому входное напряжение без потерь передается к каждой из параллельных ветвей цепи. Вольтметр V измеряет действующее значение U входного напряжения. При необходимости ток каждой ветви м рассчитать по закону Ома: ; ; . Векторную диаграмму токов строят на основе ПЗК: .Знак угла φ может быть разным в зависимости от соотношения между проводимостями B_L и B_C:1й случай B_L>B_C. При этом B=B_L–B_C>0 и, согласно (3.55), угол φ положителен (φ > 0). Из соотношения B_L>B_C следует неравенство B_LU>B_CU, т.е. I_L>I_C. Векторная диаграмма токов и напряжения изображена на рис. 3.12б. Токи и образуют реактивную составляющую , где I_р=|b_L–b_C|U. Реактивная составляющая отстает по фазе от напряжения на 90°, т.е. носит индуктивный характер. Активная составляющая , совпадающая по фазе с , равна току . Токи , и образуют треугольник токов.

комплексную мощность цепи:

где Q=BU²=(B_L–B_C)U²=X_LI_L²–X_CI_C² – реактивная мощность цепи; P=GU²=U²/R=RI_R² – активная мощность цепи. Поскольку B>0, то Q>0. Подобные ▲и проводимостей и мощностей построены на рис. 3.12в, причем учтено, что аргументом комплексной проводимости является угол «–φ».

2й случай B_L<B_C. Теперь B=B_L–B_C<0 и угол φ, согласно (3.55), становится отрицательным (φ<0). Для реактивных токов получаем неравенство I_L<I_C. На рис. 3.13а приведена диаграмма токов и напряжения цепи. Поскольку I_C>I_L, т.е. емкостная составляющая тока преобладает, то реактивная составляющая также имеет емкостный характер. Для мощностей справедливы формулы (3.60) с той лишь разницей, что теперь B, φ, Q<0, что и отражают треугольники проводимостей и мощностей на рис. 3.13б.

Рис. 3.13.

3й случай B_L=B_C. Отсюда получаем φ=0, что свидетельствует о наличии резонанса в цепи.

13.Резонанс токов. Условие возникновения резонанса. Резонансные кривые. Области применения. Коэффициент мощности Эл цепи и его народохозяйственное значение.

. Из равенства проводимостей следует равенство B_LU=B_CU, т.е. I_L0=I_C0. Векторная диаграмма токов и напр-я цепи при резонансе показана на рис. 3.13в. Из диаграммы, ток совпадает по фазе с напр-ем, как и д б при резонансе. Резонанс в парал цепи - резонансом токов.Раскроем усл-е резонансаB_L=B_C: ; ; .

Т.о, усл-е резонанса токов для цепи на рис. 3.12а совпадает с условием X_L=X_C резонанса напряжений в последовательном контуре.

Рассмотрим подробнее свойства реактивной части цепи на рис. 3.12а, т.е. контура, состоящего из параллельно включенных L- и C-элементов. Из векторной диаграммы видно, что входной ток I_р=I_L0+I_C0 этого идеального LC-контура при резонансе равен нулю, что указывает на бесконечно большое резонансное сопротивление Z_к контура. Это м док-ть: . При резонансе в знаменателе Z_к имеется 0, т.е. Z_к=∞. Частотная хар-ка полного сопротивления идеального LC-контура. Z_к(ω)=|X(ω)|, построенная по выражению (3.62), изображена на рис.3.14а. На рис. 3.14б показаны частотные характеристики токов I_L(ω), I_C(ω), I_p(ω), построенные по выражениям I_L(ω)=U/(ωL); I_C(ω)=ωCU; I_p(ω)=|I_L(ω)-I_C(ω)|; а на рис. 3.14в – частотная характеристика входного тока I(ω), построенная по выражению , где I_R=U/R=const.

Рис. 3.14. Частотные характеристики параллельного колебательного контура

В электронике применяют параллельные контуры, состоящие из катушки индуктивности и конденсатора с малыми потерями, приближающиеся по своим свойствам к идеальному параллельному LC-контуру. Благодаря свойству не пропускать резонансный ток параллельный LC-контур называют «фильтром – пробкой».

Коэф мощности -отношение активной мощности к полной, численно равен косинусу угла сдвига фаз φ между напряжением и током цепи .