Восьмеричная и шестнадцатеричная системы счисления
Позиционную систему счисления можно построить по любому основанию. Однако наибольшее практическое значение имеют: двоичная, десятичная, восьмеричная и шестнадцатеричная. Причем, последние две используются, в основном, не для вычислений, а для представления двоичного кода в форме, удобной для человека.
В табл. 2.4 представлено 24-битное двоичное слово и соответствующие ему 8-ричный и 16-ричный коды.
Таблица 2.4
Двоичный код |
1011001111000101100010112 |
Восьмеричный код |
547426138 |
Шестнадцатеричный код |
B3C58B16 |
Очевидно, что человеку легче воспринимать двоичный код в форме 8-ричного или 16-ричного кодов. При использовании 8-ричного кода три бита двоичного слова преобразуются в один символ. При использовании 16-ричного слова каждые четыре бита двоичного слова преобразуются в один символ. В табл. 2.5 показано, как осуществляется это преобразование. Как можно видеть, шестнадцатеричные числа обозначаются с помощью 10 арабских цифр и шести букв латинского алфавита.
Таблица 2.5
8-ричное число
|
Бинарный код |
16-ричное число
|
Бинарный код |
0 1 2 3 4 5 6 7
|
000 001 010 011 100 101 110 111
|
0 1 2 3 4 5 6 7 8 9 A B C D E F |
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
Лекция № 3. Фракталы
3.1. Канторово множество
Математика изобилует парадоксальными объектами. Одним из них является канторово множество. Оно описывается следующим образом. Рассмотрим единичный отрезок, показанный на рис. 3.1. Удалим из него открытую среднюю часть (1/3, 2/3) оставив два отрезка длины 1/3. Затем применим ту же самую процедуру к этим отрезкам, т.е. удалим их средние части. Продолжая процесс индуктивно до бесконечности, получим троичное канторово множество.
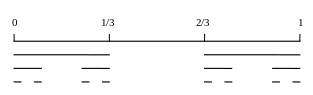
Рис. 3.1. Троичное канторово множество
Канторово множество можно построить не только геометрически, но и аналитически. Оно является совокупностью таких чисел из отрезка [0, 1], которые могут быть записаны в троичной системе счисления без использования цифры 1.
Доказательство. Интервал (1/3, 2/3) – это в точности множество чисел, у которых в первом разряде после запятой стоит 1 (при записи в троичной системе), т.е. которые в троичной системе не могут быть записаны в виде 0,0… или 0,2… (заметим, что 1/3 можно записать как 0,02222…, а 2/3 как 0,20000…). Соответственно средние части оставшихся отрезков – в точности те числа, для которых второй разряд после запятой должен быть равен 1, и т.д.
Троичное канторово множество обладает удивительными свойствами. Оно вполне несвязно, однако одновременно оно несчетно.
Доказательство.
Сопоставляя каждой точке
,
(
)
число
,
мы определяем отображение (функцию),
потому что все двоичные разложения
можно представить в таком виде. Образ
канторова множества несчетен,
следовательно, и само это множество
несчетно. Функция
представлена на рис. 3.1. Она называется
канторовой
лестницей.
Рис. 3.2. Канторова лестница
В англоязычной литературе канторову лестницу называют «лестницей дьявола» (devil stairs). Этот термин возник из-за необычной ситуации – график этой функции полностью состоит из «ступенек», а именно горизонтальных отрезков на дополнительных интервалах, но все же разрывов эта функция не имеет – она непрерывна. Таким образом, сами ступеньки на лестнице имеются, но вот их боковые грани отсутствуют. Тем самым мы получаем удивительный пример функции с некоторыми экзотическими свойствами. Микроскопическая структура канторовой лестницы точно такая же, как и глобальная структура; она не станет более простой в любом другом уменьшенном масштабе. Линии, обладающие подобными свойствами, называются фракталами. Представленный на рис. 3.1 график канторовой лестницы был построен с использованием следующей программы MATLAB.
for k=1:1023
Sum=0;
for i=1:10
p=floor(k/(2^(10-i)));
if rem(p,2)==0
b(i)=0;
else
b(i)=1;
end
Sum=Sum+b(i)/(3^i);
end
x(k)=2*Sum;
y(k)=k/1024;
end
plot(x, y)