Лекция № 2. Системы счисления

1. Позиционные и непозиционные системы

Системой счисления называется метод записи чисел в виде комбинаций графических символов. Число – это некоторая абстрактная сущность для описания количества, а цифры – знаки, используемые для записи чисел. В наше время самыми распространёнными являются арабские цифры, менее распространены римские цифры. Система римских цифр основана на употреблении особых знаков для десятичных разрядов: I=1, X=10, C=100, M=1000 и их половин: V=5, L=50, D=500. Существует множество других способов записи чисел. Например, древние греки использовали для этой цели буквы своего алфавита, а древние шумеры – клинописные знаки. Существуют позиционные и непозиционные системы счисления.

Позиционная система счисления – система записи чисел в виде последовательности символов, в которой численное значение каждого символа зависит от его положения в записи.

Примером позиционной системы является хорошо известная десятичная система счисления. Примером непозиционной системы – римская система. Выполнение арифметических действий над числами в непозиционной системе весьма неудобно. Поэтому позиционные системы в настоящее время получили наибольшее распространение.

Изобретение позиционной системы приписывается шумерам и вавилонянам. Затем она была развита индусами. В средневековой Европе позиционная десятичная система появилась благодаря итальянским купцам, которые заимствовали её у мусульман. В 9 веке великий арабский математик Мухаммед ибн Мусе Аль Хорезми впервые описал десятичную систему исчисления и правила выполнения простых арифметических действий в ней. В 12 веке его работы были переведены на латинский язык, благодаря чему Европа смогла познакомиться с этим изобретением человеческого ума.

2. Десятичная система

Существуют различные позиционные системы исчисления, отличающиеся между собой количеством используемых знаков. Чтобы различать числа в разных системах исчисления, в конце числа ставят индекс – символ системы. Например, запись означает обычное число 483,56 в десятичной системе счисления, а запись означает совсем другое число (хотя и похожее по виду) в шестнадцатеричной системе счисления (в десятичной оно равно 1155,335938). Если из контекста понятно, что используется только десятичная система (или только шестнадцатеричная, или какая-нибудь другая), то при записи числа индекс обычно опускают.

Десятичная система использует десять различных знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – которые обозначают натуральные числа в порядке их возрастания от нуля до девяти. Число 10 является основанием десятичной системы. Оно не имеет специального знака, а обозначается с помощью двух первых символов этой системы.

Например, запись 483,56 в десятичной системе означает, что данное число складывается из четырех сотен ( ), восьми десяток ( ), трех единиц ( ), пяти десятых частей единицы ( ) и шести сотых частей единицы ( ). Другими словами, мы можем записать:

. (2.1)

3. Двоичная система

Двоичная (бинарная) система счисления является самой простой из всех позиционных систем. Она содержит только два символа 0 и 1, и используется в компьютерной технике благодаря своей простоте и высокой надежности. Двоичная система была изобретена великим немецким ученым Готфридом Вильгельмом Лейбницем (1646-1716), который использовал ее в созданной им механической счетной машине. В первом столбце табл. 2.1 приведены десятичные числа, а во втором – соответствующие им двоичные числа.

Таблица 2.1

Десятичное число	Бинарный код	Код Грея	Десятичное число
0 1 2 3 = 2 + 1 4 5 = 4 +1 6 = 4 + 2 7 = 4 + 2 + 1 8 9 = 8 + 1 10 = 8 + 2 11 = 8 + 2 + 1 12 = 8 + 4 13 = 8 + 4 + 1 14 = 8 + 4 + 2 15 = 8 + 4 + 2 + 1	0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111	0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000	0 1 2 = 3 – 1 3 4 = 7 – 3 5 = 7 – 3 +1 6 = 7 – 1 7 8 = 15 – 7 9 = 15 – 7 + 1 10 = 15 – 7 + 3 – 1 11 = 15 – 7 + 3 12 = 15 – 3 13 = 15 – 3 + 1 14 = 15 – 1 15

Предположим, что нам нужно преобразовать двоичное число с дробной частью 1100,1011 в более привычное десятичное число. В табл. 2.2 показано, как осуществляется такое преобразование.

Таблица 2.2

Двоичное число								Десятичное число
Целая часть				Дробная часть
1	1	0	0,	1	0	1	1
	+	+	+	+	+	+	+	=

Обратное преобразование десятичного числа d в двоичное число (бинарный код) осуществляется в соответствии со следующим алгоритмом. Присваиваем числу d индекс ( ), и ищем целое число , удовлетворяющее неравенству

, . (2.2)

Если , то задача выполнена – искомое двоичное число содержит единицу в старшем разряде и нулей за ней.

Если , то вычисляем разность , и ищем для нее соответствующее число , пользуясь формулой (2.2) с . Операцию вычисления разницы и нахождения повторяем до тех пор, пока при каком-либо не выполнится условие: .

Очевидно, что (т.е. ). При построении искомого бинарного числа используют правило: численные значения соответствуют разрядам бинарного кода, в котором стоят единицы. Остальные разряды заполняются нулями.

Используем это правило для нахождения бинарного кода десятичного числа 108,5. Согласно формуле (2.2), получаем: .

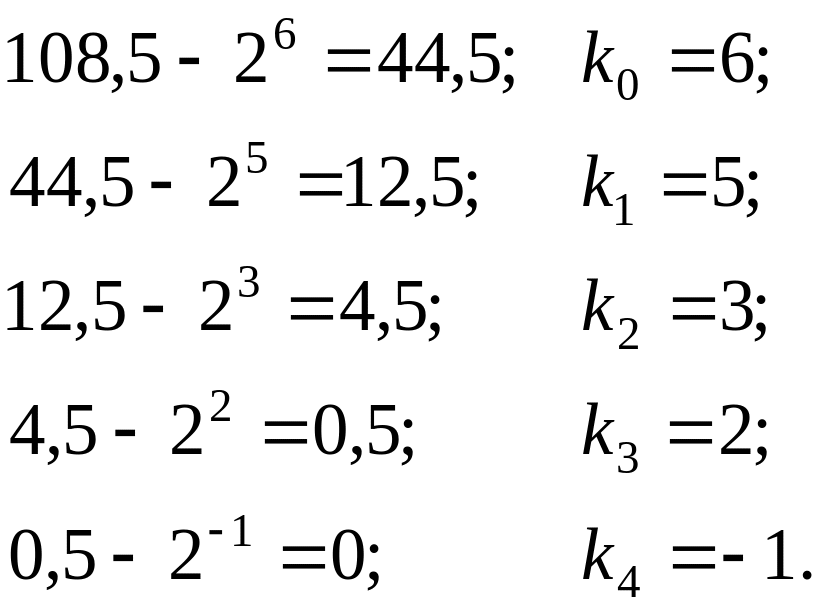
Искомое двоичное число равно: 1101100,1. Первая единица слева в записи числа соответствует 6 разряду, вторая за ней – пятому разряду. Четвертого разряда нет, поэтому за двумя первыми единицами записываем ноль. Третий и второй разряды есть – после нуля записываем две единицы. Единичного и нулевого разрядов также нет – после двух единиц записываем два нуля. Минус первый разряд есть – поэтому после запятой записываем единицу.

Арифметические операции в двоичной системе осуществляются так же, как и в десятичной («столбиком»). Например, возьмем числа 0111 ( ) и 0101 ( ), и произведем операции сложения и умножения:

,

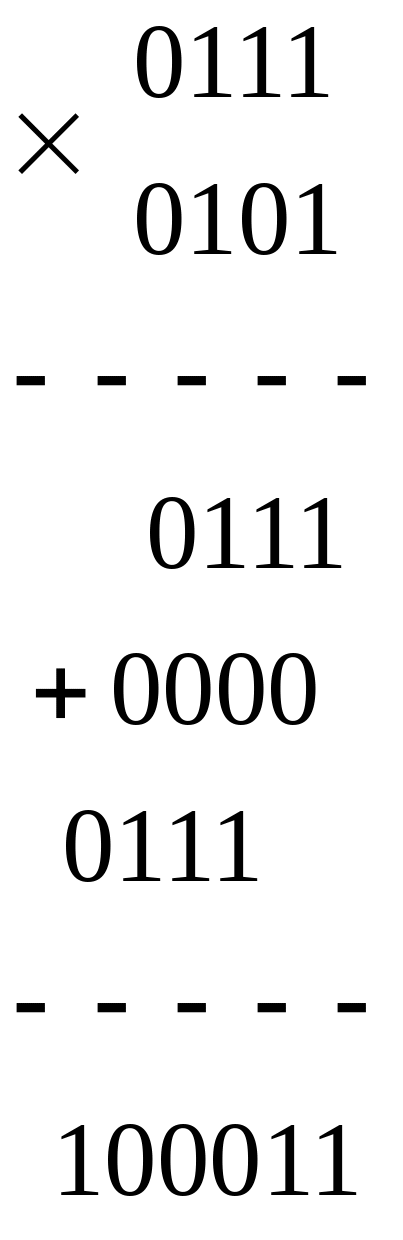
В результате получим 1100 ( ) и 100011 ( ), что и следовало ожидать.