21. Непрерывность дифференцированных ф-ий.

Ф-я называется дифференцированной в некоторой точке, если она имеет в этой точке конечную производную, при этом процесс поиска производной называется дифференцированием. Ф-я дифференцируема в некотором числовом мн-ве, если она дифференцируема в каждой точке этого мн-ва. Если y=f(x) дифференцируема в некоторой точке х0, то она в этой точке непрерывна. Замечание! Обратное утверждение неверно!

22. Правила дифференцирования ф-ии.

ТЕОРЕМА1 Если ф-ии U=U(x), V=V(х) дифференцируема в точке х0, то в этой точке также дифференцируема их алгебраическая сумма. (U V)

(U±V)ʹ=Uʹ±Vʹ Док-во: (U+V)ʹ=Uʹ+Vʹ. Обозначим у= U+V, тогда у(х0)=U(x0) +V(x0), y(x0+ x)= U(x0+∆x) +V(x0+∆x). ∆y=y(x0+∆x)-y(x0)= U(x0+∆x)+V(x0+∆x)-(U(x0)+V(x0))=[U(x0+∆x)- U(x0)]+[V(x0+∆x)-V(x0)]= ∆U+∆V. yʹ=(U+V)ʹ= lim∆x→0 ∆y/∆x= lim∆x→0 ∆U+∆V/∆x= lim∆x→0 ∆U/∆x+ lim∆x→0 ∆V/∆x= Uʹ+Vʹ.

ТЕОРЕМА2Если ф-ии U=U(x), V=V(х) дифференцируемы в точке х0, то дифференцируемо и их произведение.(U*V)

(U*V)ʹ=UVʹ+UʹV Док-во:

Следствие: (c*U)ʹ=c*Uʹ, c=const., (c*U)ʹ=cʹ*U+c*Uʹ(cʹ=0)

ТЕОРЕМА3 Если ф-ии U=U(x), V=V(х) дифференцируема в точке х0, то в этой точке также дифференцируемо их отношение.(U/V)

(U/V)ʹ=(UʹV-UVʹ)/V² Док-во:

23. Производная сложной ф-ии.

Теорема: Пусть дана сложная ф-я у=f(U), U=U(x). Если ф-я f(U) дифференцирована в точке U0, а ф-ия U(x) дифференцируема в точке х0(U0=U(x0)), то сложная ф-ия у=f(U(x)) также дифференцируема в точке х0 и справедлива формула: уʹ_х=f ʹ(U)*Uʹ(x) или уʹ_х=уʹ_u*Uʹ_x Док-во: По условиям теоремы f(U) и U(x)-дифференцируемы, т.е.: lim∆u→0 ∆y/∆U=yʹ_u и lim∆x→0 ∆U/∆x=Uʹ_x. yʹ_x=lim∆x→0 ∆y/∆x= lim∆x→0 ∆y/∆U*∆U/∆x= lim∆x→0 ∆y/∆U*lim∆x→0 ∆U/∆x= lim∆u→0 ∆y/∆U*lim∆x→0 ∆U/∆x=yʹ_u*Uʹ_x. U(x)-дифференцируема, следовательно непрерывна, значит ∆U при ∆x→0. yʹ_x=yʹ_u*Uʹ_x

24. Производная обратной функции.

у = f (x)-дифференц-ма и строго монотонна

х = g(у)-обратная к ней

Теорема: Для дифференцируемой ф-ии с производной не равной 0, производная обратной ф-ии равна обратной величине производной данной ф-ии.

25. Таблица производных.

1) С’=0; 2) (a^x)’=a^xlna; 3) (x^a)’=a*x^a-1, aϵR; 4) (e^x)’=e^x; 5) (log_ax)’=1/xlna; 6) (lnx)’=1/x; 7)(sinx)’=cosx; 8) (cosx)’=-sinx; 9) (tgx)’=1/cos²x; 10)(ctgx)’= -1/sin²x; 11) (arcsinx)’=1/ ; 12) (arcosx)’= -1/ ; 13) (arctgx)’=1/(1+x²); 14) (arcctgx)’= -1/(1+x²); 15) (shx)’=chx; 16) (chx)’=shx; 17) (thx)’=1/ch²x; 18) (cthx)’= -1/sh²x.

26. Производная ф-ии, заданной параметрически (с док-вом). 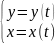. y’(x)= . x(t) – дифференцируема, => непрерывна, ∆x→0 при ∆t→0. y’(x)= y’(t)/ x’(t)

27. Логарифмическое дифференцирование ф-ий.

Логарифмическая производная ф-ии у=f(х) называется производная от логарифма этой ф-ии.

(ln f(x))ʹ=f ʹ(x)/ f (x) Последовательное применение логарифмирования и дифференцирования ф-ии называется логарифмическим дифференцированием. В ряде случаев это процесс поиска производных. Например, у=U^V(прологарифмировать)