42. Правило Лапиталя

Правило Лопиталя. Пусть ф-ция f(x) и g(x) имеет в окр. т-ки х0 пр-ные f‘ и g‘ исключая возможность саму эту т-ку х0. Пусть lim(хх )=lim(xx)g(x)=0 так что f(x)/g(x) при xx0 дает 0/0. lim(xx0)f‘(x)/g‘(x)  (4), когда он совпадает с пределом отношения ф-ции lim(xx0)f(x)/g(x)= lim(xx0)f‘(x)/g‘(x) (5)

44.1.(Критерий монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на

(a,b), и имеет в каждой точке производную f'(x). Тогда

1)f возрастает на (a,b) тогда и только тогда, когда

2) убывает на (a,b) тогда и только тогда, когда

2. (Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда

1) если то f строго возрастает на (a,b);

2) если то f строго убывает на (a,b).

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место.

3. (Критерий строгой монотонности функции, имеющей производную на интервале) Пусть и всюду на интервале определена производная f'(x). Тогда f строго возрастает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:

1)

2)

45.Необходимое и достаточное условие экстремума

Необходимые условия существования локальных экстремумов

Лемма Ферма. Пусть функция дифференцируема в точке локального экстремума x0. Тогда:

f'(x0) = 0.

Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.

Достаточные условия существования локальных экстремумов

Пусть функция непрерывна в и существуют конечные или бесконечные односторонние производные . Тогда при условии x0 является точкой строгого локального максимума. А если то x0 является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке x0

Пусть функция f непрерывна и дважды дифференцируема в точке x0. Тогда при условии

и

x0 является точкой локального максимума. А если то x0 является точкой локального минимума.

  

    

 

46. Выпуклость и вогнутость, свойство графика функции у = f (x) (кривой), заключающееся в том, что каждая дуга кривой лежит не выше (не ниже) своей хорды; в первом случае график функции f (x) обращён выпуклостью книзу (вогнутостью кверху) и сама функция называется выпуклой (рис. 1, а), во втором — график обращён вогнутостью книзу (выпуклостью кверху) и функция называется вогнутой (рис. 1, б). Если существуют производные f ¢(x) и f ²(х), то первый случай имеет место при условии, что f ²(x) ³ 0, а второй при f ²(x) £ 0 (во всех точках рассматриваемого промежутка). Выпуклость (книзу) можно охарактеризовать также тем, что дуга кривой лежит не ниже касательной, в окрестности любой своей точки (рис. 2, a), а вогнутость (книзу) — тем, что дуга кривой лежит не выше касательной (рис. 2, б). Аналогично определяются В. и в. поверхности.

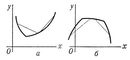рис2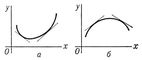 рис1

47. Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

Определение 7.1 Вертикальной асимптотой графика функции y=f(x)называется вертикальная прямая х=а если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции f(x) , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где .