16.Обратная матрица. Алгебраические дополнения

Обратная матрица.

Обратной матрице к квадр. матрице А наз. такая матрица А-1, что А-1×А = А× А-1 = Е

Замечание: если А-1 существует, то она единственная. Присоединенной матрицей к квадр. матрице А(ij) наз. матрица полученная транспонированием из матрицы составленной из алгебраических дополнений Аij для элементов аij. Минором элемента аij определителя n-порядка наз. определитель n-1-порядка полученный путем вычеркивания i-строки и j-столбца; обозначают Мij. Алгебраическим дополнением Аij для элем. аij наз. выр. вида Аij = (-1)i+j×Mij. Замечание: если i+j четное число, то Аij = Мij. Если i+j нечет.,то Аij = -Мij. Матрица А наз. невыраженное, если её определитель ≠ 0 и выраженной в противопол.случае. Теорема: если квадр. матрица не выражена, т.е. det A ≠ 0, то А-1 = 1/detА × А

Алгебраическое дополнение. Алгебраическим дополнением Аij для элемента квадратной матрицы аij называется минор этого элемента, взятый со знаком (-1)i+j .

19.Ранг Теорема Кронекера-Капелли

Ранг матрицы. Ранг матрицы – наибольший из порядков миноров матрицы, отличных от 0

Теорема: при элементарных преобразованиях ранг матрицы не меняется Теорема: ранг ступенчатой матрицы = кол-ву ненулевых строк.

Теорема Кронекера-Капелли. Для совместности необходимо и достаточно чтобы ранг матрицы равнялся расшир. матрицы. r(A) = r(A|B). Совместное СЛАУ имеет единственное реш,, если r(A) = числу неизвестных. r(A)=n. И бесконечное множество реш. r(A) < n

если r(A|B)> r(A)-система несовместна.

Очевидно, что система ( может быть записана в виде:

x1 + x2 + … + xn

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

17.Решение слау с помощью обр.Матрицы

Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы

.

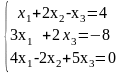Решение.

Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).

Вычислим определитель данной системы :

,

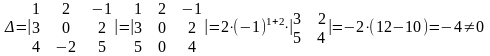следовательно, система имеет единственное решение.

Данную систему можно записать в матричной форме :

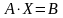, где , , .

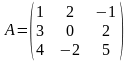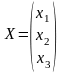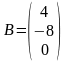Так как 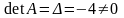, то для матрицы 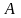существует обратная матрица 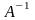. Умножив матричное уравнение слева на , получим 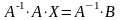, откуда 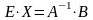, или .

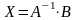Найдем обратную матрицу по формуле

,

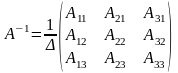где 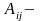алгебраическое дополнение элемента .

,

.

.

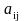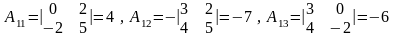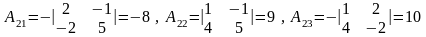
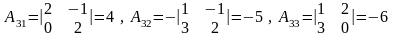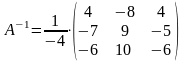Тогда

.

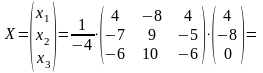
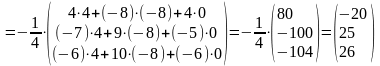Ответ : .

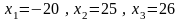18.Система м- линейных ур-ий с п неизвестными(м<п)

Системой m линейных уравнений с n неизвестными называется система вида

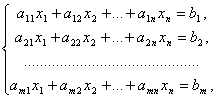
где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы 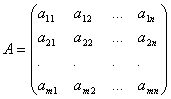, которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.

2. Система может иметь бесконечное множество решений. Например, 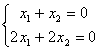. Решением этой системы является любая пара чисел, отличающихся знаком.

3. И третий случай, когда система вообще не имеет решения. Например, 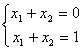, если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.