4. Расчет наклонных сечений на действие изгибающего момента.

Рис. 11.13. К расчету по наклонным сечениям

на действие изгибающего момента

Для этого случая прочность по наклонному сечению будет достаточна, если изгибающий момент М от внешних нагрузок относительно центра тяжести бетона сжатой зоны сечения (точка D) не превосходит суммы моментов внутренних усилий в продольной арматуре, хомутах и отгибах, пересекаемых той же трещиной относительно той же моментной точки.

Расчет наклонных сечений на действие изгибающего момента производят в местах обрыва или отгиба продольной арматуры в пролете, а также в приопорной зоне балок у свободного края консолей.

Обрываемые стержни должны быть заведены за место своего теоретического обрыва согласно эпюре изгибающих моментов на некоторую длину , на протяжении которой в наклонных сечениях отсутствие обрываемых стержней компенсируется поперечной арматурой, т.е. внешний момент становится равным несущей способности сечения без учета обрываемых стержней.

Условие: не менее 2 стержней должны быть доведены до опоры.

5. Кубиковая и призменная прочность бетона. Применение их значений при проектировании жбк.

Из всех прочностных характеристик бетона наиболее просто определяется его прочность при сжатии, а высокое сопротивление бетона сжатию является его ценным свойством, используемым в железобетонных конструкциях. Поэтому за основную характеристику прочностных и деформативных свойств бетона принята его прочность на осевое сжатие.

Для оценки кубиковой прочности применяют раздавливание на прессе изготовленных в тех же условиях, что и реальные конструкции кубов бетона. За стандартные образцы принимают кубы размерами150х150х150 мм, испытание которых происходит при температуре 20 ± 2 ºC через 28 дней твердения в нормальных условиях.

Опытами установлено, что прочность бетона одного и того же состава зависит от размера куба: если кубиковая прочность бетона для базового куба с ребром 150 мм равно R (рис. 2.4), то для куба с ребром 200 мм оно уменьшается до 0,93 R, а для куба с ребром 100 мм – увеличивается до 1,1 R.

Рис. 2.4. Стандартный бетонный образец для определения прочности на сжатие

Различное временное сопротивление сжатию образцов разной формы объясняется влиянием сил трения, возникающих между гранями образца и опорными плитами пресса, а также неоднородностью структуры бетона.

Вблизи опорных плит силы трения, направленные внутрь образца, создают обойму, следовательно, увеличивается прочность образцов при сжатии. Удерживающее влияние сил трения по мере удаления от торцов снижается, таким образом, бетонный куб при разрушении получает форму двух усеченных пирамид, обращенных друг к другу вершинами (рис. 2.5, а). При уменьшении сил трения посредством смазки характер разрушения меняется (рис. 2.5, б): вместо выкалывания с боков образца пирамид происходит раскалывание его по трещинам, параллельным направлению действия усилия. При этом временное сопротивление бетона сжатию уменьшается.

а) б)

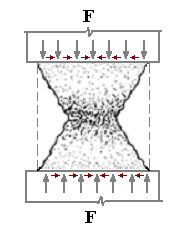
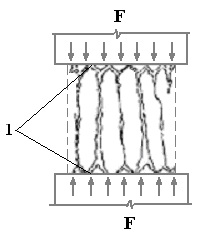
Рис. 2.5. Схема деформирования бетона при сжатии

а) – при наличии трения по опорным плоскостям;

б) – при отсутствии трения;

1 – смазка

Поскольку железобетонные конструкции по форме отличаются от кубов, в расчетах их прочности не может быть непосредственно использована кубиковая прочность бетона.

Основной характеристикой прочности бетона сжатых элементов является призменная прочность R_b.

Опыты на бетонных призмах со стороной основания а и высотой h показали, что призменная прочность R_b меньше кубиковой R и она уменьшается с увеличением отношения .

При призменная прочность становится почти стабильной и равной примерно R_b ≈ 0,75 R. Как и для кубиков, это явление объясняется различной степенью влияния сил трения по торцам образцов – чем больше размер образца и больше расстояние между его торцами, тем меньше влияние сил трения. Влияние гибкости бетонного образца становится ощутимым при .

Кривая, приведенная на рис. 2.6, иллюстрирует зависимость от по усредненным опытным данным.

Таким образом, призменная прочность R_b – это временное сопротивление осевому сжатию призмы R_bu с отношением сторон .

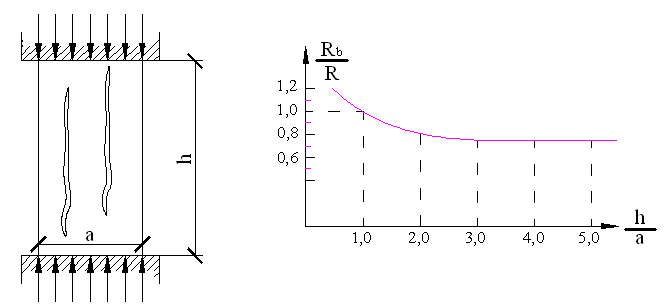
Рис. 2.6. График зависимости призменной прочности бетона от отношения