2. Расчет по наклонным сечениям для случая разрушения от действия поперечной силы.

В реальных конструкциях нагрузка q в пределах наклонной трещины может отсутствовать. Поэтому нормы предписывают учитывать уменьшение поперечной силы за счет нагрузки q, расположенной в пределах наклонного сечения лишь в тех случаях, когда она является безусловно действующей (например, давление грунта или воды).

Технологически отгибы устанавливать сложно, поэтому их применяют крайне редко. Таким образом, расчет наклонных сечений рассмотрим при условии, что .

Тогда уравнение (11.1) будет иметь вид:

(11.3)

По СНиП 2.03.01-84* «Бетонные и железобетонные конструкции» и по СП 52-101-03 «Бетонные и железобетонные конструкции без предварительного напряжения» поперечное усилие, воспринимаемое бетоном, равно

(11.4)

где 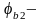коэффициент, учитывающий тип бетона (для тяжелого бетона );

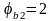коэффициент, учитывающий влияние сжатых полок (свесы) в тавровых и двутавровых элементах:

;

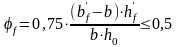принимают в зависимости от отношения высоты полки к полной высоте.

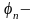коэффициент, учитывающий влияние продольных сил.

Значение .

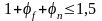При соблюдении условия 11.4 расчет наклонных сечений на прочность по поперечной силе не производят.

Рис. 11.7. К расчету по наклонным сечениям для случая разрушения

от действия поперечной силы

Уравнение 11.3 можно преобразовать, учитывая что

поперечное усилие в хомутах:

,

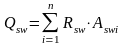где 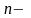количество поперечных стержней, которые пересекает опасная наклонная трещина в опасном наклонном сечении.

Но так как величина дискретная, а непрерывная функция, то в расчетах используют интенсивность .

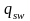Таким образом, получаем

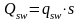
При действии усилий на проекции наклонной трещины с:

Тогда уравнение 11.3 имеет вид

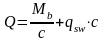(11.5)

Длина проекции расчетного опасного сечения устанавливается из условия:

тогда

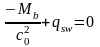
Проекция опасного наклонного сечения:

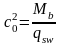, т.е.

Рассмотрим случай, когда . Тогда формула (11.5) преобразуется в следующее выражение:

,

т.е. (11.6)

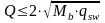– несущая способность наклонного сечения

Алгоритм решения:

1. Проверка прочности по наклонным сечениям от разрушения между наклонными трещинами:

;

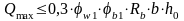2. Проверка необходимости в установке поперечных стержней (хомутов) по расчету:

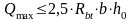
Если условие выполняется, то бетон сопротивляется внешней нагрузке без помощи хомутов.

Если условие не выполняется, необходимо установить по расчету поперечную арматуру;

3. Находим шаг стержней исходя из условия, что

– максимальный шаг стержней по конструктивным требованиям;

– наибольшее значение проекции наклонной трещины на продольную ось элемента в случае, если наклонная трещина проходит между смежными поперечными стержнями и вся поперечная сила воспринимается лишь бетоном.

;

;

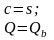
4. Определяем М_b;

5. Определяем ;

6. Подбираем диаметр и количество стержней фактической поперечной арматуры , где

7. Находим ;

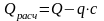8. Проверяем прочность наклонного сечения