Выбор модели регрессии и оценка параметров модели множественной регрессии.
Пусть на основе проведенного анализа поля корреляции была принята модель вида:
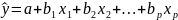(1).
Для оценки параметров регрессии применим
МНК. С этой целью составим функцию S
по параметрам и будем ее минимизировать.
.
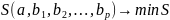Уравнение
(1) примем в виде:
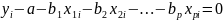
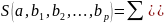
Вычислим частные производные функции S по каждому из параметров и приравняем к 0. В результате чего, получим:
Решая
эту систему методом Гауса либо методом
Крамера, получим финальную зависимость
для вычисления параметров модели.
Следует иметь в виду, что, если коэффициент
при факторах в модели множественной
регрессии рассматриваются в качестве
степени влияния факторов на показатель,
то они несравнимы. Их численные значения
зависят от выбранного. Чтобы коэффициенты
были сравнимы, модель регрессии следует
привести к стандартизованному виду,
где коэффициенты являются стандартными.
Для этого их выражают через безразмерные
стандартизированные единицы измерения
при помощи следующих соотношений:
;
.
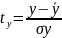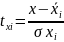Поэтому
в стандартном уравнении свободный член
a
будет отсутствовать, а уравнение будет
вида:
,
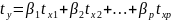где β – коэффициенты в стандартизированном
масштабе. Каждый коэффициент β вычисляется:
.
На практике иногда используют уравнение регрессии в стандартизированном масштабе:
.
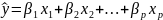Какая бы не была принята модель, после оценки параметров ее необходимо исследовать на значимость в целом и по параметрам и проверить выполнение предпосылок МНК. Имеющая значимость в целом и по параметрам может быть применена для статического анализа и прогнозов.
Предпосылки мнк.
Коэффициент модели регрессии, их свойства зависят от свойств случайной составляющей. Поэтому для того чтобы модель была значимой необходимо для нее проверять предпосылки МНК:
Математическое ожидание случайного отклонения
,
т.е. = 0. M(
)=0.
Данное условие означает, что случайное
отклонение в среднем не оказывает
влияние на y.
В каждом наблюдении
может быть как положительное, так и
отрицательное значение, но он не должен
иметь систематического смещения.Дисперсия случайных отклонений постоянна: D(
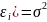для любых наблюдений i.
Данное условие подразумевает, что
несмотря на то что при каждом наблюдении
случайное отклонение может быть либо
большим, либо меньшим не должно быть
какой-либо заведомой большой ошибки.Случайное отклонение и
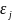для множества наблюдаемых значений.
Выполнение этого условия означает, что
отсутствует систематическая тесная
связь между любыми отклонениями. Если
условие выполняется, то говорят об
отсутствии автокорреляции в факторах.Случайное отклонение должно быть независимо от объясняющих переменных - обычно это предпосылка выполняется автоматически, если регрессионный анализ был проведен корректно.
Модель регрессии является линейной относительно параметров. Предпосылка должна удовлетворять теореме Гауса-Маркова, согласно которой она должна отвечать следующим свойствам:
- оценки являются не смещенными – говорит об отсутствие систематической ошибки
- оценки состоятельны, т.к. дисперсия параметров при увеличении наблюдений стремится к нулю
- оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров.