11. Оценка модели нелинейной парной регрессии на значимость.

Для того чтобы модель регрессии могла быть использована для статистического анализа и прогноза, она должна быть значима и с этой целью использован индекс корреляции:

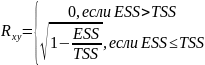
Индекс корреляции всегда принимает значение 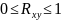, причем, чем больше 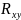ближе к 1, тем значимо уравнение регрессии. Причем, если при линеаризации затрагивается только фактор, то индекс корреляции совпадает с парным коэффициентом изучаемого показателя и преобразованным фактором, т.е. 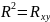. Близость индекса и коэффициента детерминации означает, что нет необходимости усложнять модель и даже может быть использована модель, приведенная к линейному виду. Затем используют критерий Фишера и вычисляется F статистика: , где n – число наблюдений, m – число параметров при факторе.

Затем по таблице находится табличное значение F статистики.

12. Множественная регрессия.

Представляет собой регрессию результативного признака-показателя с 2 и большим числом независимых переменных-факторов. В общем случае записывается: 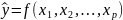, но поскольку при моделировании достаточно сложно учесть все факторы и однозначно определить их статистическую связь с показателем используется уравнение следующего вида: , где - отклонение результативного значения от его теоретического, найденного по уравнению регрессии. Все факторы входят в уравнение со своими коэффициентами, значение которых, как и в парной регрессии, могут быть найдены МНК, но при соблюдении определенных условий. При исследовании зависимости показателя от ряда факторов решаются те же задачи, что и в парной: определение вида регрессии, оценка параметров, определение вида и тесноты связи между фактором и показателем. Могут использоваться как линейные, так и нелинейные модели регрессий. В отличии от парной регрессии для получения статистического значения модели, которая может быть применена для анализа и прогнозов, является отбор факторов.

13. Отбор факторов при построение множественной регрессии.

Осуществляется в несколько этапов:

1. Факторы должны быть количественно измеримы. (Желательно в одних единицах измерения, если этого невозможно, то факторы выражаются в процентом отношении по степени влияния на показатель)

2. Факторы должны показывать, как они влияют на показатель по отдельности и в совокупности. Влияние фактора на показатель должно подтверждаться индексами корреляции факторов с показателями.

3. Факторы не должны находится в тесной связи друг с другом. Для этого проводится межфакторная корреляция и включение в модель факторов с коэффициентами корреляции близкими к единицы, может привести к нежелательным последствиям:

- они будут дублировать друг друга, что влечет затруднения экономической интерпретации параметров модели

- применение МНК для оценки параметров модели дает неправильный результат и влечет за собой ненадежность и статистически незначимые модели.

Если будет установлен коэффициент корреляции 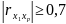, то один из факторов в модели не стоит включать. Какой из них решает исследователь, если же при этом между некоторыми двумя факторами близок к 1, то это обуславливает мультипликативность модели, что отвергает применение линейной модели регрессии.

4. Включенные в модель факторы должны объяснять изменение изучаемого показателя, т.е. вариацию его. Долю вариации определяет коэффициент детерминации, который должен возрастать с включением в модель каждого нового фактора, если этого не происходит, то фактор, включенный в модель не правомерно.

5. Число включенных в модель факторов должно быть в 6-7 раз меньше числа наблюдений, по которым строится регрессия.

Если отсутствует линейная корреляция меж факторами, то определитель будет равен 1. Если определитель равен 0, то меж факторами есть мультиколлинеарность. Для выявления, которой надо проанализировать парные коэффициенты меж факторной корреляции. Если они больше 0,7, то один из факторов из модели удалить.