8. Оценка модели по параметрам.

Оценки модели по параметрам осуществляется по критерию Стъюдента. С этой целью, по каждому параметру вычисляют стандартную ошибку:

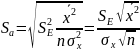,где σ – среднее квадратическое отклонение.

.

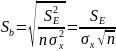Далее вычисляется статистика Стъюдента:

;

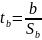
По таблицам находится табличное значение статистики Стъюдента. Если

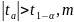
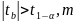
(m = n - 2– число степеней свободы), то делается вывод, что параметры модели значимы с уровнем значимости α.

Если модель регрессии окажется значимой в целом и по параметрам, то ее можно применять для статистического анализа и прогноза.

Если модель окажется незначима в целом, то нет смысла ее оценивать на значимость по параметрам.

Если модель незначима по параметрам или одному параметру, то она не может применяться для анализа и прогнозов. В этом случае необходимо изменить специфику модели и в частности нелинейную и весь процесс эконометрического исследования применить сначала.

9. Нелинейная парная регрессия.

Для оценки параметров нелинейной модели регрессии используется 2 похода:

- основанный на линеаризации модели (привидение к линейному виду) с помощью подходящих преобразований;

- основанный на том, что применяют нелинейные методы оптимизации, в случае, когда линеаризовать модель не возможно.

Для линеаризации модели при первом подходе могут использоваться модели нелинейные по параметру, так и по переменным. Если модель нелинейна по переменным, то введя соответствующие замены, ее легко к линейной модели и тогда для оценки параметра модели используется обычный МНК.

Если между экономическими величинами имеется нелинейная связь, то исследователю-экономисту прежде чего следует определиться с видом выбранной модели.

Чаще всего используются:

- регрессии нелинейные по объясняемым параметрам, но линейные по оцениваемым параметрам – это, как правило, полиномы различных степеней

ŷ=a+b₁x+b₂x²+b₃x³+

-равносторонняя гипербола ŷ=a+b/x+

Регрессии нелинейные по оцениваемым параметрам:

- степенная ŷ = ax^b+

- показательная ŷ = ab^x+ , ŷ = ab^x

- экспоненциальная ŷ = е^a+bx+ .

Опыт эконометрических исследований показывает, что в случае использования полиномиальной модели редко используется полином степени выше 3.

С помощью замены переменных x₁=x; x²=x₂; x³=x₃

ŷ = a+b₁x+b₂x₂+b₃x₃+ . Для нахождения параметров легко используется МНК.

Дифференцируем функцию по каждому из параметров легко получим систему нормальных уравнений, преобразовав которую придем к следующей системе:

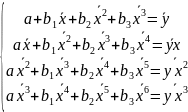
В случае, если для некоторой полиномиальной модели число уравнений в системе будет равно числу неизвестных, то значение параметров проще найти методом Крамера, где 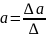, , 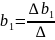, 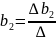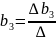. Δ – определитель матрицы системы, 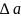, ,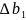 , 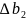– определители параметров составленные с заменой соответствующего столбца на столбец свободных членов.

10. Регрессии нелинейные по оцениваемым параметрам.

Эти модели подразделяются на 2 типа:

- нелинейные модели внутринелинейные

- нелинейные модели внутриненелинейные

Если модель внутринелинейна, то она с помощью преобразований может быть приведена к линейному виду.

Если модель внутриненелинейна, то ее нельзя привести к линейному виду.

- степенная, где - закупаемое количество продукта, x – цена, – случайная ошибка. Это модель считается внутринелинейной, т.к. логарифмируют ее по основанию е, получим линейную модель вида:

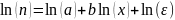
К линейной модели легко применить МНК и путем соответствующих преобразований получить финальные зависимости при оценке параметров

;
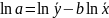