Средние показатели рядов динамики.
Средний уровень – определяется делением сумм уровней на их число
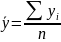
В
моментном ряду динамики с равноотстоящими
датами времени
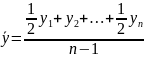
Средний абсолютный прирост – отношение сумм цепных абсолютных приростов на их число
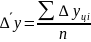
Средний темп роста
Экстраполяция на основе средних значений временных рядов.
Предположим,
что средний уровень ряда не имеет
тенденции к изменению или это изменение
не значительное, можно принять, что
,
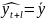т.е. среднее значение прогнозированного
уровня равно среднему значению уровней
в прошлом. Доверительные границы для
средних при небольшом числе наблюдений
определяется:
,
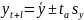где
-
табличное значение статистики Стъюдента,
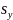-средняя
квадратическая ошибка, вычисляется по
формуле:
.
Доверительный
интервал для прогностической оценки:
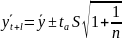
Доверительные интервалы и экстраполяция по скользящей и экспоненциальной средней.
Для
краткосрочного прогнозирования могут
использоваться скользящие средние.
Если прогнозирование ведется на один
шаг вперед
,
-
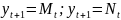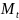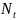адаптивная скользящая средняя,
-
экспоненциальная скользящая средняя.
Здесь
доверительный интервал для скользящей
средней можно определить:
;
,
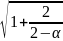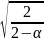α – коэффициент сглаживания от 0 до 1.
Примерное
значение коэффициента сглаживания
определяется:
,
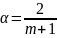m
– число уровней ВР, входящих в интервал
сглаживания.
Экстраполяция на основе среднего темпа.
Если
в основу экстраполяции положен средний
темп роста, то экстраполированное
значение уровня можно получить
,
где
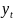- база экстраполяции,
-
темп роста. Экономический процесс
развивается по геометрической прогрессии
либо по экспоненциальной прямой. Этот
вид экстраполяции нарушает основное
допущение о том, что развитие будет
следовать основной тенденции – тренд.
Статистическая надежность выше
приведенных методов оценивается с
помощью коэффициента вариации
,
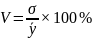где σ – среднее квадратическое отклонение.
Метод считается статистически значимым,
если значение коэффициента вариации
не превышает 10%.