
- •Вопросы к экзамену по эконометрике:
- •Парная регрессия.
- •Множественная регрессия.
- •Оценка влияния количественных показателей друг на друга.
- •Линейная парная регрессия.
- •Оценка параметров модели.
- •Оценка значимости модели регрессии.
- •Оценка модели регрессии в целом.
- •Оценка модели по параметрам.
- •Нелинейная парная регрессия.
- •Регрессии нелинейные по оцениваемым параметрам.
- •Оценка модели нелинейной парной регрессии на значимость.
- •Множественная регрессия.
- •Отбор факторов при построение множественной регрессии.
- •Выбор модели регрессии и оценка параметров модели множественной регрессии.
- •Предпосылки мнк.
- •Проверка предпосылок мнк.
- •Анализ временных рядов экономических процессов.
- •Требования, предъявляемые к временным рядам.
- •Цель статистического анализа временных рядов.
- •Этапы построения прогноза по временным рядам.
- •Предварительный анализ данных.
- •Критерий нисходящих и восходящих серий.
- •Сглаживание временных рядов.
- •Метод простой скользящей средней.
- •Метод взвешенной скользящей средней.
- •Метод экспоненциального сглаживания.
- •Моделирование тенденции временных рядов.
- •Моделирование тренда при наличии сезонной компоненты.
- •Сущность метода последовательных разностей.
- •Сущность метода отклонения от тренда.
- •Сущность метода включения в модель фактора времени.
- •Моделирование сезонной компоненты временного ряда.
- •Определение циклической составляющей.
- •Прогнозы по регрессионным моделям и моделям временного ряда.
- •Показатели, рассчитываемые на основе временных рядов (рядов динамики).
- •Средние показатели рядов динамики.
- •Экстраполяция на основе средних значений временных рядов.
- •Доверительные интервалы и экстраполяция по скользящей и экспоненциальной средней.
- •Экстраполяция на основе среднего темпа.
Вопросы к экзамену по эконометрике:
Парная регрессия.
Связывает
изученный показатель с одним фактором
и может представляться: y=ŷ(x)+ ,
где
– остаток или возмущение, характерное
отклонение модели регрессии от его
теоретического значения.
,
где
– остаток или возмущение, характерное
отклонение модели регрессии от его
теоретического значения.
определяется количеством и качеством изученных при моделировании факторов.
В эконометрике используются следующие основные типы парной регрессии:
Ŷ=a+bx - линейная
Ŷ=a+bx+cx2 - квадратичная
Ŷ=a+b/x - гиперболическая
Ŷ=axb - степенная
Ŷ=a+bx - показательная
Парная регрессия относится к простой, поскольку использует только один фактор, поэтому в процессе исследований реальных экономических систем, в которых используется много факторов, более применимы модели множественной регрессии.
Множественная регрессия.
Основными типами множественной регрессии являются:
Ŷ=a0+a1x1+a2x2+…+apxp - линейная
Ŷ=a0+a1x+a2x2+…+apxp - степенная
Ŷ=еa+b1x1+b2x2+…+bpxp - экспоненциальная
Где a0, a, b1, b, b2, bp – параметры регрессии, подлежащие нахождению и оценки в ходе эконометрического исследования.
Выбор той или иной модели регрессии должен основываться на корреляционном анализе и оценке качества модели регрессии.
Чем сложнее модель регрессии, тем хуже интерпретируется ее параметры к реальной ситуации. Увеличение числа параметров в модели при наличии достаточно малых количества данных приводит к статистически несущественности (незначимости модели).
Оценка влияния количественных показателей друг на друга.
Использование линейной модели в эконометрическом анализе оправдано только в том случае, если имеет место сильная, тесная связь изучаемого показателя с факторами. Изучить влияние показателя с фактором с помощью коэффициент корреляции:
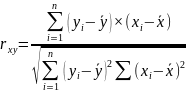 (1)
(1)
Поскольку
для применения формулы (1) предварительно
нужно вычислить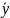 ,
,
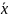 и поэтому чаще пользуются другой
формулой:
и поэтому чаще пользуются другой
формулой:
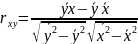 (2)
(2)
Для применения формул (1) и (2) целесообразно рассчитать и заполнить таблицу 1.
i – количество наблюдений.
-
i
y
x
x*y
y2
x2
Δy
Δx
Δy*Δx
1
y1
x1
x1*y1
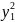

-
-
-
2
y2
x2
x2*y2

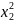
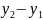
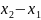
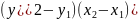
3
y3
x3
x3*y3

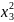
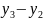

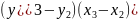
…
…
…
…
…
…
…
…
…
n
yn
xn
xn*yn
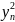
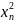
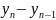

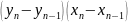
Σ
Σyi
Σxi
Σxiyi
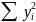



ср.знач
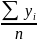
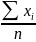
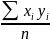
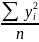
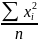
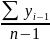
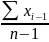
Коэффициент корреляции обладает следующими свойствами:
 ≤ 1
≤ 1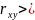 0,
то имеется прямая связь между фактором
и показателем, в противном случае связь
обратная.
0,
то имеется прямая связь между фактором
и показателем, в противном случае связь
обратная.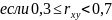 ,
то связь слабая
,
то связь слабая
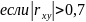 ,
то связь сильная или тесная.
,
то связь сильная или тесная.
Однако по вычисленному коэффициенту корреляции нельзя судить об истинности или ложности связи, поэтому необходимо вычислять коэффициент корреляции по первым разностям. Коэффициент по первой разности вычисляется по формуле:

Если
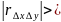 0,3, то связь между фактором и показателем
истинная.
0,3, то связь между фактором и показателем
истинная.
