35.Влияние концентрации напряжений на прочность при циклическом нагружении.

Одним из основных факторов, которые необходимо учитывать при практических расчетах деталей на циклическую прочность, является концентрация напряжений. Исследования показывают, что в области резких изменений в форме упругого тела (внутренние углы, отверстия, выточки), а также в зоне контакта деталей возникают повышенные напряжения.

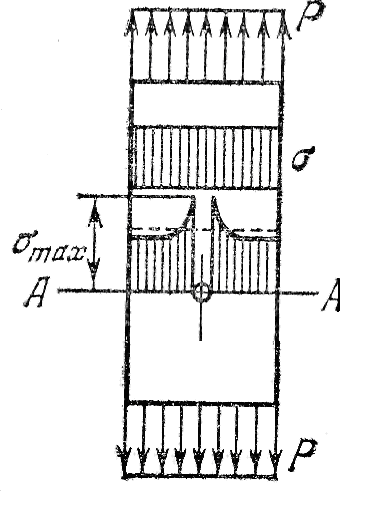
Описанная особенность распределения напряжений получила название концентрации напряжений. Зона повышенных напряжений ограничена узкой областью очага концентрации, и в связи с локальным характером распространения эти напряжения называются местными. Основными показателями местных напряжений являются теоретические коэффициенты концентрации напряжений:

для нормальных напряжений

α_σ =σ_max / σ_ном

для касательных напряжений (кручение вала)

α_τ =τ_max / τ_ном

где σ_max и τ_max — наибольшие местные напряжения, σ_ном и τ_ном — так называемые номинальные напряжения. установить соотношение между эффективным и теоретическим коэффициентами концентрации в виде

К_σ = 1+q(α_σ – 1)

где q — так называемый коэффициент чувствительности материала к местным напряжениям.

36. Коэффициент запаса.

Учитывая свойства материала конструкции напряжение определяется по схеме σ_mах = σ_L/n где σ_L - некоторое предельное для данного материала напряжение, n — число, большее единицы, называемое коэффициентом запаса или просто запасом. фактический коэффициент запаса: n = σ_L/ σ_mах Если этот запас удовлетворяет требованиям, считается, что поверочный расчет дал положительный результат. Выбор величины σ_L чаще всего зависит от эксплуатационных требований.Если необходимо избежать заметных остаточных деформаций, за величину σ_L для пластичных материалов принимается обычно предел текучести. Тогда наибольшее рабочее напряжение составляет n-ю долю от σ_т или σ_тр . Коэффициент в этом случае обозначается через n_т и называется коэффициентом запаса по текучести. Для хрупких, а в некоторых случаях и для умеренно пластичных материалов за σ_L принимается предел прочности σ_вр или σ_вс соответственно получаем n_в= σ_вр/ σ_mах где n_в — коэффициент запаса по пределу прочности. Если расчет ведется по предельной нагрузке, то аналогично может быть введено понятие запаса по предельной нагрузке n= P_L/ Р_раб где P_L и Р_раб -— предельная и рабочая нагрузки. Если расчет ведется на жесткость n= δ_L/ δ_раб ; где δ_L и δ_раб — предельное и рабочее перемещения.

38. Коэффициент Пуассона.

Экспериментально установлено, что в пределах применимости закона Гука поперечная деформация пропорциональна продольной,

ε_попер=μ ε_прод

где μ —безразмерный коэффициент пропорциональности, называемый коэффициентом Пуассона. Величина μ характеризует свойства материала и определяется экспериментально. Для всех металлов числовые значения μ лежат в пределах 0,25-0,35 и вообще не может превышать 0,5.

39. Закон Гука.

перемещения в определенных пределах пропорциональны действующим силам. Эта закономерность была дана Гуком в 1660 году в формулировке «каково удлинение, такова сила».

Если рассмотреть перемещение произвольно взятой точки А по некоторому направлению, например по оси х, то

UА= δ_Х P

где Р — сила, под действием которой происходит перемещение и_А, а δ_X — коэффициент пропорциональности между силой и перемещением

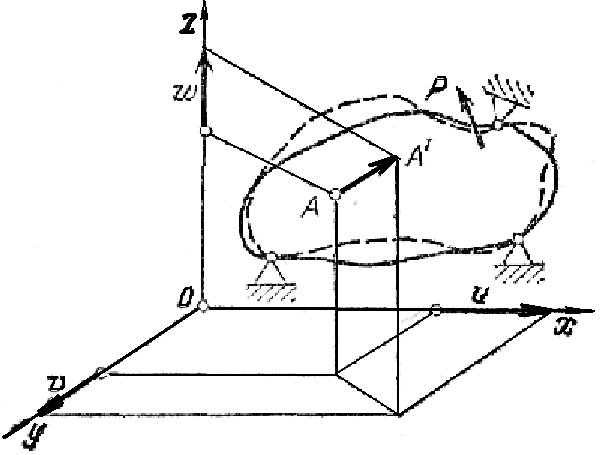Очевидно, этот коэффициент зависит как от физических свойств материала, так и от взаимного расположения точки А и точки приложения силы. Таким образом, выражение следует рассматривать как закон Гука для системы. Коэффициенты пропорциональности в этом случае представляют собой физические константы материала и уже не связаны с геометрическими особенностями системы в целом. Закон, таким образом, выражает свойства самого материала. . γ _α = 2 (1+μ) τ_α /Е. Это соотношение в случае изотропного материала является единым для всех типов напряженных состояний и носит название закона Гука для сдвига.