Закон эквивалентов

       Еще до создания атомно–молекулярного учения было установлено, что простые и сложные вещества вступают в химические реакции в строго определенных массовых соотношениях.

Закон эквивалентов: Все вещества реагируют и образуются в эквивалентных соотношениях.

Эквивалентное соотношение означает одинаковое число моль эквивалентов. Т.о. закон эквивалентов можно сформулировать иначе: число моль эквивалентов для всех веществ, участвующих в реакции, одинаково.

Квантово-механическая модель атома

В 1924 г. французский физик Луи де Бройль высказал идею о том, что материя обладает как волновыми, так и корпускулярными свойствами. Согласно уравнению де Бройля (одному из основных уравнений квантовой механики),

т. е. частице с массой m, движущейся со скоростью v соответствует волна длиной λ; h — постоянная Планка.

Длину волны такой частицы называют длиной волны де Бройля. Для любой частицы с массой т и известной скоростью v длину волны де Бройля можно рассчитать. Идея де Бройля была экспериментально подтверждена в 1927 г., когда были обнаружены у электронов как волновые, так и корпускулярные свойства. В 1927 г. немецким ученым В. Гейзенбергом был предложен принцип неопределенности, согласно которому для микрочастиц невозможно одновременно точно определить и координату частицы X, и составляющую р_х импульса вдоль оси х. Математически принцип неопределенности записывают следующими уравнениями:

ΔxΔp_x ≥ h;

ΔxΔp_y ≥ h;

ΔxΔp_z ≥ h.

Отсюда следует, что при точном определении координаты х микрочастицы исчезает информация о ее импульсе Δp_x, так как при х=0 величина Δp_x→∞. Если удастся снизить погрешность Δp,то будет велика погрешность Δх. Источник этих погрешностей заключен не в приборах, а в самой природе вещей.

Поскольку постоянная Планка очень мала, то ограничения, накладываемые принципом неопределенности, существенны только в масштабах атомных размеров. Согласно принципу неопределенности, невозможно утверждать, что электрон, имеющий определенную скорость, находится в данной точке пространства, здесь можно использовать лишь вероятностное описание.

Для описания свойств электрона используют волновую функцию, которую обозначают буквой Ψ (пси). Квадрат ее модуля |Ψ|², вычисленный для определенного момента времени и определенной точки пространства, пропорционален вероятности обнаружить частицу в этой точке в указанное время. Величину |Ψ|² называют плотностью вероятности. Наглядное представление о распределении электронной плотности атома дает функция радиального распределения. Такая функция служит мерой вероятности нахождения электрона в сферическом слое между расстояниями r и (r+dr) от ядра. Объем, лежащий между двумя сферами, имеющими радиусы r и (r+dr), равен 4Πr²dr, а вероятность нахождения электрона в этом элементарном объеме может быть представлена графически в виде зависимостей функции радиального распределения. На рис. 1 представлена функция вероятности для основного энергетического состояния электрона в атоме водорода. Плотность вероятности |Ψ|² достигает максимального значения на некотором конечном расстоянии от ядра. При этом наиболее вероятное значение r для электрона атома водорода равно радиусу орбиты a₀ соответствующей основному состоянию электрона в модели Бора. Различная плотность вероятности дает представление об электроне, как бы размазанном вокруг ядра в виде так называемого электронного облака (рис. 2).

 

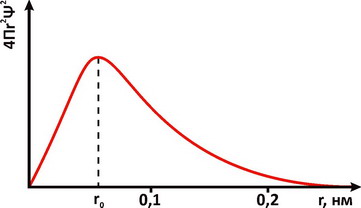
Рис. 1. Радиальное распределение  вероятности пребывания электрона для основного энергетического состояния атома водорода

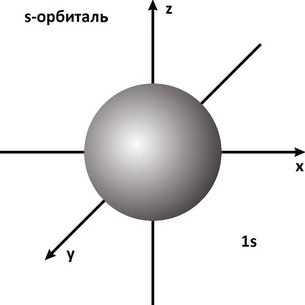
Рис. 2. Электронное s-облако (l - 0)

 

Чем больше величина |Ψ|², тем больше вероятность нахождения электрона в данной области атомного пространства.

В квантовой механике вместо термина «орбита» используют термин «орбиталь», которым называют волновую функцию электрона. Соответственно орбиталь характеризует и энергию и форму пространственного распределения электронного облака. Расчеты в квантовой механике проводят с помощью предложенного в 1926 г. австрийским ученым Э. Шредингером уравнения, которое является математическим описанием электронного строения атома в трехмерном-пространстве.

В простейшем случае уравнение Шредингера может быть записано в виде

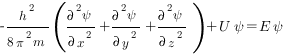
где h — постоянная Планка; m — масса частицы; U — потенциальная энергия; Е — полная энергия; х, у, z — координаты; Ψ — волновая функция.

Решая уравнение Шредингера, находят волновую функцию Ψ=f(x, y, z). Решение уравнения Шредингера возможно лишь при определенных значениях полной энергии Е. Определив вероятностную функцию можно оценить величину |Ψ|²dV — вероятность нахождения электрона в объеме пространства dV, окружающего атомное ядро. Решение уравнения Шредингера представляет сложную математическую задачу.

Электронные орбитали-это энергетические уровни,на которых вращаются электроны.

Формы электронных орбиталей

В зависимости от энергии электронные облака отличаются размерами и формой.  Сферическая s- орбиталь симметрична относительно ядра и не имеет выделенного направления.  Гантелеобразные р- орбитали расположены под прямым углом друг к другу вдоль трех осей координат (x,y,z) - Px,Py,Pz.  Электроны, которые находятся на s-орбитали называют s- электронами, на р- орбитали - р- электронами.  Орбитали более сложных форм обозначаются буквами d,f.

Электронные уровни s подуровни имеют 1 энергетическую ячейку (в ячейке может быть максимум 2 электрона), т.е. на данных подуровнях может быть максимум 2 электрона  p подуровни имеют 3 энергетические ячейки, т.е. на данных подуровнях может быть максимум 6 электронов  d подуровни имеют 5 энергетических ячеек, т.е. на данных подуровнях может быть максимум 10 электронов  f подуровни имеют 7 энергетических ячеек, т.е. на данных подуровнях может быть максимум 14 электронов  Дальше. Заполнение электронами орбиталей в атоме происходит по правилу Клечковского, если Вы школьник то можете не читать правило, а знать всего лишь последовательность:  1s > 2s > 2p > 3s > 3p > 4s > 3d > 4p > 5s > 4d > 5p > 6s > 4f > 5d > 6p > 7s > 5f > 6d > 7p  Еще одно правило Хунда. В каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон.  Дальше. Допустим вы написали актиний номер 89 (порядковый номер показывает сколько протонов и электронов у данного элемента). Задача распределить эти электроны по ячейкам.  Смотрим на последовательность вначале видим заполняется 1s, в соответствии с тем что написано выше 2 электрона мы ставим на 1s-подуровень и вычитаем из 89 два электрона которые теперь находятся на 1s-подуровне 89 - 2 = 87.  Смотрим дальше на последовательность видим что дальше заполняется 2s-подуровень, в соответствии с тем что написано выше 2 электрона мы ставим на 2s-подуровень и вычитаем из 87 два электрона которые теперь находятся на 2s-подуровне 87 - 2 = 85.  И т.д. 

Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

1. Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n = 1, 2, 3, . . .)

2. Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1(l = 0, 1, 2, 3,..., n-1). Каждому значению l соответствует орбиталь особой формы. Орбитали с l = 0 называются s-орбиталями,  l = 1 – р-орбиталями (3 типа, отличающихся магнитным квантовым числом m),  l = 2 – d-орбиталями (5 типов),  l = 3 – f-орбиталями (7 типов).

3. Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от +l до -l, включая 0. Например, при l = 1 число m принимает 3 значения: +1, 0, -1, поэтому существуют 3 типа  р-АО:  р_x,  р_y,  р_z.

4. Спиновое квантовое число s может принимать лишь два возможных значения +1/2 и -1/2. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемого спином (от англ. веретено). Для обозначения электронов с различными спинами используются символы: 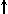  и  .

Принцип запрета Паули утверждает, что в одном квантовом состоянии могут находиться не более двух тождественных фермионов. В связи с этим: 1)на каждом уровне имеется 2n² состояний, где n - главное квантовое число(принимает значения: 1,2,3,..). 2)на подуровне имеется 2(2L+1) состояний, где L - орбитальное квантовое число(принимает значения: 0,1,2,..,n-1). 

Правило Хунда определяет порядок заполнения орбиталей определённого подслоя и формулируется следующим образом: модуль суммарного значения спинового квантового числаэлектронов данного подслоя должен быть максимальным. Сформулировано Фридрихом Хундом в 1925 году.

Это означает, что в каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон. При этом на одной орбитали находятся два электрона с полуцелыми спинами противоположного знака, которые спариваются (образуют двухэлектронное облако) и, в результате, суммарный спин орбитали становится равным нулю.

Другая формулировка: Ниже по энергии лежит тот атомный терм, для которого выполняются два условия.

1. Мультиплетность максимальна

2. При совпадении мультиплетностей суммарный орбитальный момент L максимален.

Принцип наименьшей энергии

Максимальная устойчивость атома (как системы) соответствует ми­нимуму его полной энергии. В атоме каждый электрон стремится за­нять положение, соответствующее минимальному значению энергии, что отвечает наибольшей его связи с ядром. Последовательность заполнения энергетических уровней и подуровней в атоме электронами происходит в

Соответствии с принципом наименьшей энергии.

Энергия электрона в основном определяется главным квантовым числом П И побочным /, поэтому сначала заполняются те подуровни, для которых сумма значений квантовых чисел П И / является меньшей.

Например, запас энергии на подуровне 4S Меньше, чем на 3d, Так как в первом случае П+1 = 4+0 = 4, а во втором П+1 = 3+2 = 5; на 5S Уровне меньше, чем на Ad, Так как запас энергии на 5S Уровне равен «+/ = 5+0 = 5 < 4+2 = 6.

В случае, когда для двух подуровней суммы значений П И / равны, сначала идет заполнение подуровня с меньшим значением П. Так, на подуровнях 3d, Ар, 5S Сумма значений П И / равна 5. В данном случае происходит сначала заполнение подуровней с меньшими значениями П, А именно: 3DAР5S. Из этого правила встречаются некоторые исклю­чения, когда энергии близких подуровней очень мало отличаются друг от друга. Например, подуровень 5D Заполняется одним электроном 5D Раньше, чем Af.

Заполнение электронами энергетических уровней и подуровней происходит в следующей последовательности:

\s2 -> 2s2 -> 2Р6 -> 3s2 -> Зр6 -> 3s2 -> 3d10 -> Ар6 -> 5/ -> Ad10 -> ->5 Р 6 -> 6s2 -> 5Й?1 -> А/4 -> 5<i2"10 -> бР6 -> 7/ -> бй?1 -> 5/14 -> 6<i2"10 -> ^7 Р .

3.6. Правило Гунда

Заполнение ячеек электронами происходит по правилу Гунда, со­гласно которому В пределах подуровня электроны располагаются сна­чала каждый в отдельной ячейке (в виде так называемых «холостых»

- валентных электронов), затем, когда все ячейки данного подуровня окажутся занятыми, начинается уплотнение электронов вновь по­ступающими, т. е. происходит их «спаривание». Иначе говоря, элек­троны в пределах данного подуровня (S, P, D, F) Заполняются таким об­разом, чтобы суммарный спин был максимальным. Например, если в трех Р-ячейках (атома азота) необходимо распределить три электрона, то они будут располагаться каждый в отдельной ячейке: в этом случае суммарный спин равен 3/2, но не так, когда суммарный спин S = + 1/2

- 1/2 + 1/2 = 1/2. Сложение спинов производится по правилу сложения векторов, так как спин электрона, определяющий величину собствен­ного момента количества движения электрона, является вектором.

Следовательно, заполнение энергетических уровней в атоме про­исходит таким образом, что при обычном состоянии атомов в первую очередь заполняются наиболее низкие энергетические уровни (табл. 3.1). В целом строение электронных оболочек атомов связано с перио­дической системой элементов.