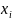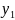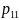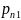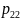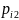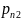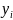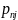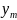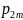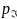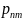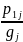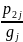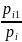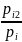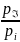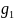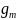- •1.Предмет теории вероятности
- •2 Важных правила комбинаторики:
- •2. События и их классификация
- •3 Соотнешения между событ-ми.
- •6. Теоремы сложения и умножения вер-тей
- •18.Нормальн.З-н распред.Непрер.Св.Вероятн.Попад.Знач.Норм.Случ.Величины в зад.Полуинтервал.
- •20.Функция одной случайной величины.Матем.Ожид.Функц.Одной св
- •21.Функция двух случайны аргументов
- •22. Понятие системы св. Закон распределения двумерной св, условный закон распред-ия двумерной св.
- •23. Числ. Хар-ки системы дискрет. Св (мат. Ожид, дисперсия, ковариация, коэффициент лин-ой корреляции и его св-ва).
- •24. Закон больших чисел. Неравенства Маркова и Чебышева.
- •27. Статистические оценки параметров распределения
- •28 Выбороч хар-ки статистич распред.
- •29. Точечные и интервальные оценки параметров распределения. Доверительная вероятность (надежность) и доверительные интервалы.
- •30.Доверительный интервал для математического ожидания нормального распределения при известной дисперсии
- •31. Статистическая проверка гипотез
- •38.Двухфакторный дисперсионный анализ.
- •1. В каждом наблюдении ei имеет нормальное распределение с нулевым мо и конечной дисперсией.
- •2. Для любого I дисперсия ei является величиной постоянной.
21.Функция двух случайны аргументов
Если
каждой паре возм.значений случ.величин.Х
и У соотв.одно возм.значение СВ Z
,то Z
будем называть функцией двух
случайн.аргументов Х и У.Z=φ(Х,У).На
практике часто треб.найти распред.функции
Z=Х+У
по
известным распред.слогаемых.Рассмотрим
дискретн.случай на примере:Пусть
дискр.незав.СВ Х,У заданы распред. ,
,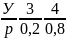 .Тогда
возможн.значения Z=Х+У
есть суммы кажд.возм.значения СВ со
всеми
возм.значен.СВУ:z1=x1+y1(1+3),z2=x1+y2(1+4),z3=x2+y1(2+3),z4=x2+y2.Найдём
вероятн.для этих значений.Для того
чтобы Z=4
дост.чтобы Х приняло значен.х1=1,а СВ У
знач.у1=3.Т.к.СВ Х,У независимы,то событ.Х=1
У=3 незав.и след.вероятн.их совм.наступл.,т.е.
вероятн.событ.Z=1+3=4
по теореме умнож.вероятн.=0,4*0,2=0,08.Аналогично
найдём
вероятн.событий:Р(Z)=1+4=5)=0,4*0,8=0,32,Р(Z=2+3=5)=0,6*0,2=0,12.Р(Z=2+4=6)=0,6*0,8=0,48.Тогда
искомое распределение(сложим
предварит.вероятн.событий)Z=Z2;Z=Z3
имеет вид
.Тогда
возможн.значения Z=Х+У
есть суммы кажд.возм.значения СВ со
всеми
возм.значен.СВУ:z1=x1+y1(1+3),z2=x1+y2(1+4),z3=x2+y1(2+3),z4=x2+y2.Найдём
вероятн.для этих значений.Для того
чтобы Z=4
дост.чтобы Х приняло значен.х1=1,а СВ У
знач.у1=3.Т.к.СВ Х,У независимы,то событ.Х=1
У=3 незав.и след.вероятн.их совм.наступл.,т.е.
вероятн.событ.Z=1+3=4
по теореме умнож.вероятн.=0,4*0,2=0,08.Аналогично
найдём
вероятн.событий:Р(Z)=1+4=5)=0,4*0,8=0,32,Р(Z=2+3=5)=0,6*0,2=0,12.Р(Z=2+4=6)=0,6*0,8=0,48.Тогда
искомое распределение(сложим
предварит.вероятн.событий)Z=Z2;Z=Z3
имеет вид
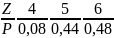 .Контроль:0,08+0,44+0,48=1.
.Контроль:0,08+0,44+0,48=1.
22. Понятие системы св. Закон распределения двумерной св, условный закон распред-ия двумерной св.
Совместное
рассмот-ие нескольких СВ приводит к
системе СВ. Рассмотрим систему двух СВ
Х и У, кот условно будем обознач. (Х,У).
Геометр-и двумерную СВ (Х,У) можно
истолковать либо как случ-ю точку М(Х,У)
пл-ти
 (т.е. точку со случ-ми координатами),
либо как случ-ый радиус вектор
(т.е. точку со случ-ми координатами),
либо как случ-ый радиус вектор
 .
.
Законом
распред-ия дискет. двумерной СВ (Х,У)
будем назыв табл в кот перечислены
возмож. знач-ия этой СВ (т.е. пары чисел
( и соответ-но им вероятность
и соответ-но им вероятность
 (i=
(i=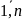 ,
j=
,
j=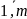 ))
))
х у |
|
|
… |
|
… |
|
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
|
1 строка табл содержит все возмож. знач-ия сост-ие Х, а 1-й столбец все возмож. знач-ия состов-ие У. В клетке стоящий на пересечении столбца
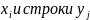 .
Того что двумерная СВ примет знач-ия
(
,
т.е.
.
Того что двумерная СВ примет знач-ия
(
,
т.е.
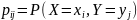 .Поскольку
событие
.Поскольку
событие
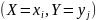 ,
i=
,
j=
образуют полную гр., то
,
i=
,
j=
образуют полную гр., то
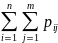 .
.
Универсальным способом задания двумерной СВ (Х,У) явл задание ее ф-ции распред. F(x,y)=P(X<x, Y<y) (1)
Опред для каждой пары чисел (Х,У) вероятность того, что Х примет знач-ие меньше х и при этом У примет знач-ие меньше у.
Геометр-и равенство (1) означает вероят-ть того, что случ-ая точка (Х,У) попадает в бесконечно прямой угол с вершиной в точке М(х,у).
Распред одной СВ (составляющей) системы (Х,У) найденное при усл. что др СВ этой системы приняла опред-ые знач-ия назыв условным законом распред этой СВ.
В
случае когда распред дискретной СВ
(Х,У) заданной табл 1 условное распределение
составляющей Х при усл что У= имеет вид :
имеет вид :
Х |
|
|
… |
|
Р |
|
|
… |
|
 =
=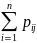 ,
j=
(1)
,
j=
(1)
Здесь вероят во второй строке табл (ряда условного распределения) получ-ся делением каждой из вероятности j-строки табл 1 на сум. всех вероятностей этой строки.
Аналогично условное распределение состав У при усл, что Х= имеет вид:
Y |
|
|
… |
|
Р |
|
|
… |
|
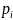 =
=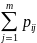 ,
i=
,
i=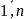 (2)
(2)
Безусловные законы распред сост-щих Х и У системы дискрет. СВ (Х,У) заданной табл 1 представляют собой табл в кот перечислены знач-ия сост-щих Х,У и их сум-ые вероят по столбцам и по строкам соответ-о:
-
Х
…
Р
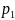
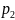
…
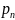
Y |
|
|
… |
|
Р |
|
|
… |
|